
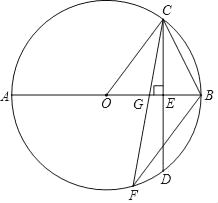
【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD于点E,BF∥OC,连接BC和CF,CF交AB于点G.
(1)求证:∠OCF=∠BCD;
(2)若CD=4,tan∠OCF=![]() ,求⊙O半径的长.
,求⊙O半径的长.
【答案】(1)证明见解析;(2)⊙O半径的长为![]() .
.
【解析】
(1)利用垂径定理得到![]() ,再根据圆周角定理得到∠BCD=∠BFC,接着根据平行线的性质得∠OCF=∠BFC,从而得到∠OCF=∠BCD;
,再根据圆周角定理得到∠BCD=∠BFC,接着根据平行线的性质得∠OCF=∠BFC,从而得到∠OCF=∠BCD;
(2)用垂径定理得到CE=![]() CD=2,再利用tan∠OCF=tan∠BCD=
CD=2,再利用tan∠OCF=tan∠BCD=![]() =
=![]() 得到BE=1,设OC=OB=x,则OE=x-1,在Rt△OCE中利用勾股定理得到x2=(x-1)2+22,然后解方程即可.
得到BE=1,设OC=OB=x,则OE=x-1,在Rt△OCE中利用勾股定理得到x2=(x-1)2+22,然后解方程即可.
(1)证明:∵AB是直径,AB⊥CD,
∴![]() ,
,
∴∠BCD=∠BFC,
∵BF∥OC,
∴∠OCF=∠BFC,
∴∠OCF=∠BCD;
(2)∵AB⊥CD,
∴CE=![]() CD=2,
CD=2,
∵∠OCF=∠BCD
∴tan∠OCF=tan∠BCD=![]() =
=![]() ,
,
∵CE=2
∴BE=1,
设OC=OB=x,则OE=x﹣1,
在Rt△OCE中,∵x2=(x﹣1)2+22,解得x=![]() ,
,
即⊙O半径的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,直角坐标平面内,小明站在点A(﹣10,0)处观察y轴,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则小明在y轴上的盲区(即OE的长度)为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知直线y=-![]() x+4与y轴交于A点,与x轴交于B点,C点坐标为(﹣2,0).
x+4与y轴交于A点,与x轴交于B点,C点坐标为(﹣2,0).
(1)求经过A,B,C三点的抛物线的解析式;
(2)如果M为抛物线的顶点,联结AM、BM,求四边形AOBM的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。

(1)判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
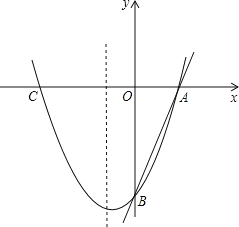
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
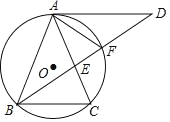
【题目】如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
(1)求∠DAF的度数;
(2)求证:AE2=EFED;
(3)求证:AD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x的函数关系式为________,自变量x的取值范为________;药物燃烧后,y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过________分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com