
【题目】如图,直线l1 :y=-3x+3与x轴交于点D,直线l2经过A(4,0)、B(3,![]() )两点,直线l1 与直线l2交于点C.
)两点,直线l1 与直线l2交于点C.
(1)求直线l2的解析式和点C的坐标;
(2)在 y轴上是否存在一点P,使得四边形PDBC的周长最小?若存在,请求出点P的坐标,若不存在,请说明理由.

【答案】(1) y=![]() x-6,点C(2,-3);(2)存在,点P的坐标为(0,-1).
x-6,点C(2,-3);(2)存在,点P的坐标为(0,-1).
【解析】
(1)将点A(4,0)、B(3,-![]() )代入y=kx+b中,用待定系数法即可求出直线l2的解析式;联立两直线的解析式即可求出点C的坐标;
)代入y=kx+b中,用待定系数法即可求出直线l2的解析式;联立两直线的解析式即可求出点C的坐标;
(2)作点D关于y轴的对称点D1,连结C D1,交y轴于一点,则该点即为要求的点P,用待定系数法求出CD1的解析式,然后可求出点P的坐标.
(1) 设直线l2的解析式为y=kx+b(k≠0),将点A(4,0)、B(3,-![]() )代入y=kx+b中,
)代入y=kx+b中,
 ,
,
解得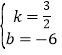 ,
,
所以直线l2的解析式为y=![]() x-6.
x-6.
联立方程组,
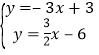 ,
,
解得![]() ,
,
∴点C(2,-3) ;
(2)存在,作点D关于y轴的对称点D1,连结C D1,交y轴于一点,则该点即为要求的点P,

在y=-3x+3中,令y=0,则x=1,即点D(1,0),点D关于y轴的对称点D1(-1,0),
∴点C(![]() ,0).
,0).
设直线C D1的解析式为y=kx+b(k≠0),将点C(2,-3)、D1(-1,0)代入,得:
得:![]() ,解得
,解得![]()
∴直线BC的解析式为y=-x-1 ,令x=0,则y=-1,
则点P的坐标为(0,-1).


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
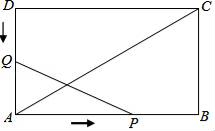
【题目】如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么:
(1)当t为何值时,△QAP是等腰直角三角形?
(2)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,点D、E分别在边AB、AC上,点F在CD上.
(1)若∠AED=∠ACB, ∠DEF= ∠B,求证:EF//AB;
(2)若D、E、F分别是AB、AC、CD的中点,连接BF,若四边形 BDEF的面积为6,试求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC三个顶点分别是A(2,0)、B(0,4)、C(-3,0),把△ABC沿x轴向右平移4个单位,得到△A1B1C1.
(1)在图中以黑点为原点建立平面直角坐标系,画出△ABC和△A1B1C1;
(2)写出A1、B1、C1各点的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 和
和![]() 中,
中,![]() ,
,![]() ,将
,将![]() 如图摆放,使得
如图摆放,使得![]() 的两条边分别经过点
的两条边分别经过点![]() 和点
和点![]() .
.

(1)当将![]() 如图1摆放时,则
如图1摆放时,则![]() _________度.
_________度.
(2)当将![]() 如图2摆放时,请求出
如图2摆放时,请求出![]() 的度数,并说明理由.
的度数,并说明理由.
(3)能否将![]() 摆放到某个位置时,使得
摆放到某个位置时,使得![]() 、
、![]() 同时平分
同时平分![]() 和
和![]() ?直接写出结论_______(填“能”或“不能”)
?直接写出结论_______(填“能”或“不能”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com