
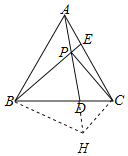
【题目】如图,等边△ABC中,点D、E分别在边BC、AC上,AE=CD,连接AD、BE交于点P.
(1)求证:∠BPD=60°.
(2)连接PC,若CP⊥PB.当AP=3,求BP的长.

【答案】(1)详见解析;(2)6.
【解析】
(1)证明△ADC≌△BEA即可说明AD=BE;证明∠BPQ=∠EBA+∠BAP=60°即可求解∠PBQ的度数;
(2)延长PD至H,使PH=BP,连接BH、CH,证明△BPH是等边三角形,得出BP=BH=PH,∠HBP=∠ABD=60°,推出∠ABP=∠CBH,由SAS证得△ABP≌△CBH得出CH=AP=3,∠BCH=∠BAP,证明CH∥BE,推出CH⊥CP,∠HPC=30°,得出PH=2CH=6,即可得出结果.
(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°,
在△ABE和△CAD中,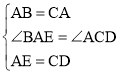 ,
,
∴△ABE≌△CAD(SAS),
∴∠ABE=∠CAD,
∵∠CAD+∠BAD=60°,
∴∠ABE+∠BAD=60°,
∴∠BPD=∠ABE+∠BAD=60°;
(2)解:延长PD至H,使PH=BP,连接BH、CH,如图所示:
∵△ABC是等边三角形,
∴AB=BC,∠BAC=∠ABC=60°,
由(1)知:∠BPD=60°,
∴△BPH是等边三角形,
∴BP=BH=PH,∠HBP=∠ABD=60°,
∴∠ABP+∠PBD=∠CBH+∠PBD,
∴∠ABP=∠CBH,
在△ABP和△CBH中,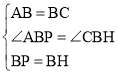 ,
,
∴△ABP≌△CBH(SAS),
∴CH=AP=3,∠BCH=∠BAP,
∵∠ABE=∠CAD,∠BAC=∠ABC=60°,
∴∠EBC=∠BAP,
∴∠BCH=∠EBC,
∴CH∥BE,
∵CP⊥PB,∠BPD=60°,
∴CH⊥CP,∠HPC=90°﹣60°=30°,
∴PH=2CH=2×3=6,
∴BP=6.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A﹙-2,-5﹚、C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙-2,-5﹚、C﹙5,n﹚,交y轴于点B,交x轴于点D.
(1)求反比例函数y=![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA、OC,求△AOC的面积;
(3)写出使一次函数的值大于反比例函数的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装店10月份以每套500元的进价购进一批羽绒服,当月以标价销售,销售额14000元,进入11月份搞促销活动,每件降价50元,这样销售额比10月份增加了5500元,售出的件数是10月份的1.5倍.
(1)求每件羽绒服的标价?
(2)进入12月份,该服装店决定把剩余羽绒服按10月份标价打九折销售,结果全部卖掉,而且这批羽绒服总获利不少于12700元,问这批羽绒服至少购进多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 为常数).
为常数).
![]() 若该二次函数的图象与两坐标轴有三个不同的交点,求
若该二次函数的图象与两坐标轴有三个不同的交点,求![]() 的取值范围;
的取值范围;
![]() 已知该二次函数的图象与
已知该二次函数的图象与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,若存在点
,若存在点![]() 使得
使得![]() 与
与![]() 面积相等,求
面积相等,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一枚均匀的正方体骰子六个面上分别标有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,如果用小刚抛掷正方体骰子朝上的数字
,如果用小刚抛掷正方体骰子朝上的数字![]() ,小强抛掷正方体骰子朝上的数字
,小强抛掷正方体骰子朝上的数字![]() 来确定点
来确定点![]() ,那么他们各抛掷一次所确定的点
,那么他们各抛掷一次所确定的点![]() 落在已知直线
落在已知直线![]() 图象上的概率是________.
图象上的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮计划暑期结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4、5、6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形OABC中,点A的坐标是(﹣3,1),点B的纵坐标是4,则B,C两点的坐标分别是( )
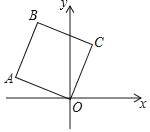
A. (﹣2,4),(1,3) B. (﹣2,4),(2,3)
C. (﹣3,4),(1,4) D. (﹣3,4),(1,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,且AC=BC,P是△ABC外接圆⊙O上的一动点(点P与点C位于直线AB的异侧)连接AP、BP,延长AP到D,使PD=PB,连接BD.
(1)求证:PC∥BD;
(2)若⊙O的半径为2,∠ABP=60°,求CP的长;
(3)随着点P的运动,![]() 的值是否会发生变化,若变化,请说明理由;若不变,请给出证明.
的值是否会发生变化,若变化,请说明理由;若不变,请给出证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com