
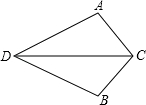
如图,点D为码头,A,B两个灯塔与码头的距离相等,DA,DB为海岸线.一轮船离开码头,计划沿∠ADB的角平分线航行,在航行途中C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.
【考点】全等三角形的应用.
【分析】只要证明轮船与D点的连线平分∠ADB就说明轮船没有偏离航线,也就是证明∠ADC=∠BDC,证角相等,常常通过把角放到两个三角形中,利用题目条件证明这两个三角形全等,从而得出对应角相等.
【解答】解:此时轮船没有偏离航线.
理由:由题意知:DA=DB,AC=BC,
在△ADC和△BDC中,
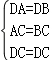 ,
,
∴△ADC≌△BDC(SSS),
∴∠ADC=∠BDC,
即DC为∠ADB的角平分线,
∴此时轮船没有偏离航线.
【点评】本题考查了全等三角形的应用,解答本题的关键是:根据条件设计三角形全等,巧妙地借助两个三角形全等,寻找对 应角相等.要学会把实际问题转化为数学问题来解决.
应角相等.要学会把实际问题转化为数学问题来解决.


科目:初中数学 来源: 题型:
如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )
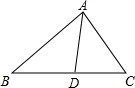
A.3:4 B.4:3 C.16:9 D.9:16
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中BD、CD平分∠ABC、∠ACB过D作直线平行于BC,交AB、AC于E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系是( )
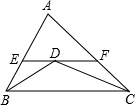
A.EF=BE+CF B.EF>BE+CF C.EF<BE+CF D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
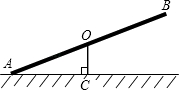
如图是标准跷跷板的示意图.横板AB的中点过支撑点O,且绕点O只能上下转动.如果∠OCA=90°,∠CAO=25°,则小孩玩耍时,跷跷板可以转动的最大角度为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com