
【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如下表所示:
国外品牌 | 国内品牌 | |
进价(元/部) | 4400 | 2000 |
售价(元/部) | 5000 | 2500 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可毛获利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
【答案】
(1)解:设商场计划购进国外品牌手机x部,国内品牌手机y部,由题意,得:
![]() ,
,
解得 ![]() ,
,
答:商场计划购进国外品牌手机20部,国内品牌手机30部;
(2)解:设国外品牌手机减少a部,则国内手机品牌增加3a部,由题意,得:
0.44(20﹣a)+0.2(30+3a)≤15.6,
解得:a≤5,
设全部销售后获得的毛利润为w万元,由题意,得:
w=0.06(20﹣a)+0.05(30+3a)=0.09a+2.7,
∵k=0.09>0,
∴w随a的增大而增大,
∴当a=5时,w最大=3.15,
答:当该商场购进国外品牌手机15部,国内品牌手机45部时,全部销售后获利最大,最大毛利润为3.15万元.
【解析】(1)设商场计划购进国外品牌手机x部,国内品牌手机y部,商场计划购进两种手机若干部,共需14.8万元和两种手机全部销售后可毛获利润共2.7万元建立方程组求出其解即可;(2)设国外品牌手机减少a部,则国内手机品牌增加3a部,表示出购买的总计金额,由用于购进这两种手机的总资金不超过15.6万元就求出a的取值范围,再设设全部销售后获得的毛利润为w万元,表示出总利润与a的关系式,由一次函数的性质就可以求出最大利润。


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】如图所示的是A,B,C,D三点,按如下步骤作图:①先分别以A,B两点为圆心,以大于 ![]() AB的长为半径作弧,两弧相交于M、N两点,作直线MN;②再分别以B,C两点为圆心,以大于
AB的长为半径作弧,两弧相交于M、N两点,作直线MN;②再分别以B,C两点为圆心,以大于 ![]() 的长为半径作弧,两弧相交于G,H两点,作直线GH,GH与MN交于点P,若∠BAC=66°,则∠BPC等于( )
的长为半径作弧,两弧相交于G,H两点,作直线GH,GH与MN交于点P,若∠BAC=66°,则∠BPC等于( )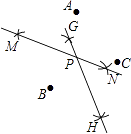
A.100°
B.120°
C.132°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.

(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面积为40,BD=5,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨,某物流公司现有26吨货物,计划A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发以每秒2cm的速度沿A→C→B运动,设点P运动的时间是t秒,那么当t=____,△APE的面积等于6.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC内有一个点P1,当P1、A、B、C没有任何三点在同一直线上时,如图1,可构成3个互不重叠的小三角形;若△ABC内有两个点P1、P2,其它条件不变,如图2,可构成5个互不重叠的小三角形:……若△ABC内有n个点,其它条件不变,则构成若干个互不重叠的小三角形,这些小三角形的内角和为()
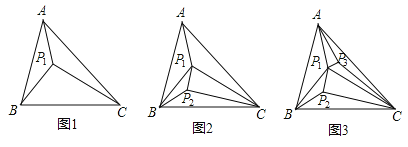
A.n·180°B.(n+2)·180°C.(2n-1)·180°D.(2n+1)·180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于50%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=70时,y=50;x=80时,y=40.
(1)求一次函数y=kx+b的表达式,并确定自变量x的取值范围.
(2)若该商场获得利润为w元,销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com