
【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象。
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?

【答案】(1)s2=-96t+2400(2)小明从家出发,经过20min在返回途中追上爸爸,这时他们距离家还有480m
【解析】
(1)首先由小明的爸爸以96m/min速度从邮局同一条道路步行回家,求得小明的爸爸用的时间,即可得点D的坐标,然后由E(0,2400),F(25,0),利用待定系数法即可求得答案;
(2)首先求得直线BC的解析式,然后求直线BC与EF的交点,即可求得答案.
解:(1)∵小明的爸爸以96m/min速度从邮局同一条道路步行回家,
∴小明的爸爸用的时间为:![]() =25(min),
=25(min),
即OF=25,
如图:设s2与t之间的函数关系式为:s2=kt+b,
∵E(0,2400),F(25,0),
∴![]() ,
,
解得:![]() ,
,
∴s2与t之间的函数关系式为:s2=-96t+2400;
(2)如图:小明用了10分钟到邮局,
∴D点的坐标为(22,0),
设直线BD即s1与t之间的函数关系式为:s1=at+c(12≤t≤22),
∴![]() 解得:
解得:![]() ,
,
∴s1与t之间的函数关系式为:s1=-240t+5280(12≤t≤22),
当s1=s2时,小明在返回途中追上爸爸,
即-96t+2400=-240t+5280,
解得:t=20,
∴s1=s2=480,
∴小明从家出发,经过20min在返回途中追上爸爸,这时他们距离家还有480m.


科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,且OA、OB分别与反比例函数y=![]() (x>0)、y=﹣
(x>0)、y=﹣![]() (x<0)的图象交于A、B两点,则tan∠OAB的值是( )
(x<0)的图象交于A、B两点,则tan∠OAB的值是( )

A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△AOB,AO=AB=5,OB=6.以O为原点,以OB边所在的直线为x轴,以垂直于OB的直线为y轴建立平面直角坐标系.

(1)求点A的坐标;
(2)若点A关于y轴的对称点为M,点N的横、纵坐标之和等于点A的横坐标,请在图中画出一个满足条件的△AMN,并直接在图上标出点M,N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,OA=OB=6,点C,D分别为线段OA,OB上的动点(C,D不与A,B重合),则AD+CD+BC的最小值为( )
,OA=OB=6,点C,D分别为线段OA,OB上的动点(C,D不与A,B重合),则AD+CD+BC的最小值为( )

A.4B.6C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
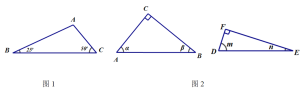
【题目】①如图1,有一个三角形,它的内角分别为:25°,50°,105°请你把这个三角形分成两个等腰三角形.画出你分割的示意图并标注必要的角度。
②如图2,有两个直角三角形,如图所示,∠C=∠F=90°,∠A, ∠B, ∠D, ∠E的度数分别是![]() ,它们互不相等。请你将这两个三角形分别分割成两个三角形,使
,它们互不相等。请你将这两个三角形分别分割成两个三角形,使![]() 所分成的两个三角形与
所分成的两个三角形与![]() 所分成的两个三角形角度对应相等。画出你分割的示意图并用字母标注必要的角度。
所分成的两个三角形角度对应相等。画出你分割的示意图并用字母标注必要的角度。
③如图3,在正方形![]() 所在平面内找一点
所在平面内找一点![]() ,使其与正方形中的每一边所构成的三角形均为等腰三角形,这样的点有________个.
,使其与正方形中的每一边所构成的三角形均为等腰三角形,这样的点有________个.
④如图4,在等边△ABC所在平面内找一点Q,使其与等边三角形中的每一边所构成的三角形均为等腰三角形,这样的点有________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划召开“诚信在我心中”主题教育活动,需要选拔活动主持人,经过全校学生投票推荐,有2名男生和1名女生被推荐为候选主持人.
(1)小明认为,如果从3名候选主持人中随机选拔1名,不是男生就是女生,因此选出的主持人是男生和女生的可能性相同,你同意他的说法吗?为什么?
(2)如果从3名候选主持人中随机选拔2名,请通过列表或画树状图求选拔的2名主持人恰好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,在边长为1的正方形网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,1),B(2,3).
(1)请在图中画出△AOB关于y轴的对称△A′OB′,点A′的坐标为 ,点B′的坐标为 ;
(2)请写出A′点关于x轴的对称点A′'的坐标为 ;
(3)求△A′OB′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△DCE有公共顶点C,AB=CD,BC=CE,∠ABC=∠DCE=90°.
(1)如图1,当点D在BC延长线上时.
①求证:△ABC≌△DCE.
②判断AC与DE的位置关系,并说明理由.
(2)如图2,△CDE从(1)中位置开始绕点C顺时针旋转,当点D落在BC边上时停止.
①若∠A=60°,记旋转的度数为![]() ,当
,当![]() 为何值时,DE与△ABC一边平行.
为何值时,DE与△ABC一边平行.
②如图3,若AB=c, BC=a, AC=b, a>c,边BC,DE交于点F,求整个运动过程中,F在BC上的运动路程(用含a, b, c的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com