

分析 (1)根据勾股定理以及算术平方根的意义即可解决问题.
(2)根据两点间距离公式计算即可.
(3)把问题转化为在x轴上找一点P(x,0),到A(0,2),B(3,1)的距离之和最小,作A关于x轴的对称点A′,连接BA′与x轴的交点即为所求的点P.此时PA+PB最小,
解答 解:(1)∵AB2=AQ2+BQ2=|x1-x2|2+|y1-y2|2=(x1-x2)2+(y1-y2)2,
∴AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$.
故答案为$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$.
(2)∵A(1,-3),B(-2,1),
∴AB=$\sqrt{(1+2)^{2}+(-3-1)^{2}}$=5.
故答案为5.
(3)代数式$\sqrt{{x}^{2}+{2}^{2}}$+$\sqrt{(x-3)^{2}+{1}^{2}}$的最小值表示在x轴上找一点P(x,0),到A(0,2),B(3,1)的距离之和最小.
如图,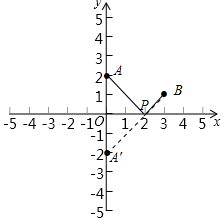
作A关于x轴的对称点A′,连接BA′与x轴的交点即为所求的点P.此时PA+PB最小,
∵A′(0,-2),B(3,1),
∴PA+PB=PA′+PB=BA′=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$.
∴代数式$\sqrt{{x}^{2}+{2}^{2}}$+$\sqrt{(x-3)^{2}+{1}^{2}}$的最小值为3$\sqrt{2}$.
点评 本题考查最短问题、勾股定理、两点间的距离公式的应用等等知识,解题的关键是灵活运用这些知识解决问题,学会用转化的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 如图是某种蜡烛在燃烧过程中高度与时间之间关系的图象,由图象解答下列问题:
如图是某种蜡烛在燃烧过程中高度与时间之间关系的图象,由图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为纪念爱国诗人屈原,我市在俯南河隆重举行了一次龙舟比赛,如图是甲、乙两支龙舟队在比赛时的路程s(米)与时间t(分钟)之间的图象,请你根据图象回答下列问题:
为纪念爱国诗人屈原,我市在俯南河隆重举行了一次龙舟比赛,如图是甲、乙两支龙舟队在比赛时的路程s(米)与时间t(分钟)之间的图象,请你根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD是正方形,△AEF是等边三角形,E、F分别位于DC边和BC边上.
如图,已知四边形ABCD是正方形,△AEF是等边三角形,E、F分别位于DC边和BC边上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将长方形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接CE.
如图,将长方形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com