
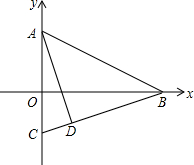
 ��ͼ����֪��ֱ��y=-$\frac{1}{2}$x+3��y�ύ�ڵ�A����x�ύ�ڵ�B����CΪy�Ḻ������һ�㣬����BC���ҡ�ABC=45�㣬BC=2$\sqrt{10}$����AD��BC������ΪD��
��ͼ����֪��ֱ��y=-$\frac{1}{2}$x+3��y�ύ�ڵ�A����x�ύ�ڵ�B����CΪy�Ḻ������һ�㣬����BC���ҡ�ABC=45�㣬BC=2$\sqrt{10}$����AD��BC������ΪD������ ��1�����ȸ���ֱ��y=-$\frac{1}{2}$x+3��y�ύ�ڵ�A����x�ύ�ڵ�B���ֱ������A��B��������Ƕ��٣�Ȼ����ֱ��BC��б����k�����ݡ�ABC=45�㣬���k��ֵ�Ƕ��٣��������ֱ��BC�Ľ���ʽ��
��2�����ȸ���MP��x�ᣬ�ɵ�$\frac{AP}{AO}=\frac{MP}{OB}$���ݴ����MP��ֵ�Ƕ��٣�Ȼ�����AD��BC����ABC=45�㣬BC=2$\sqrt{10}$�����AD��BD��DC��ֵ���Ƕ��٣��ٸ��������������ж��ķ������жϳ���AOE�ס�ADC���Ƶ�$\frac{OE}{DC}=\frac{AO}{AD}$���ݴ����OE��ֵ�Ƕ��٣�������MP��x�ᣬ�ɵ�$\frac{3-t}{3}=\frac{PN}{1}$���ݴ����PN��ֵ���������d��t֮��ĺ�����ϵʽ��������AO�ij��ȣ�����Ա���t��ȡֵ��Χ��
��3���������⣬������������ٵ���MND�ǵ��������Σ���DM=DNʱ���ڵ���MND�ǵ��������Σ���DM=MNʱ��Ȼ����ݵ��������ε����ʣ��������ۣ����t��ֵ�Ƕ��ټ��ɣ�
��� �⣺��1����ֱ��y=-$\frac{1}{2}$x+3��y�ύ�ڵ�A����x�ύ�ڵ�B��
��A��0��3����B��6��0����
��ֱ��BC��б����k��
�ߡ�ABC=45�㣬
��$\frac{k-��-\frac{1}{2}��}{1-\frac{1}{2}k}$=tan45��=1��
���k=$\frac{1}{3}$��
��ֱ��BC�Ľ���ʽ��y=$\frac{1}{3}$��x-6��=$\frac{1}{3}$x-2��
��2����ͼ1��AD��x�ύ�ڵ�E��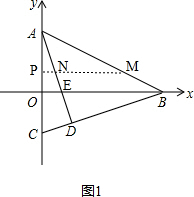
��MP��x�ᣬ
��$\frac{AP}{AO}=\frac{MP}{OB}$��
��$\frac{3-t}{3}=\frac{MP}{6}$��
��MP=6-2t��
��AD��BC����ABC=45�㣬
��AD=BD=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$��$\sqrt{{6}^{2}{+3}^{2}}$=$\frac{3\sqrt{10}}{2}$��
��DC=BC-BD=2$\sqrt{10}$-$\frac{3}{2}\sqrt{10}$=$\frac{\sqrt{10}}{2}$��
��AD��BC��
���CAD+��ACD=90�㣬
�֡ߡ�CAD+��AEO=90�㣬
���AEO=��ACD��
�ڡ�AOE�͡�ADC�У�
$\left\{\begin{array}{l}{��AOE=��ADC=90��}\\{��AEO=��ACD}\end{array}\right.$��
���AOE�ס�ADC��
��$\frac{OE}{DC}=\frac{AO}{AD}$��
��$\frac{OE}{\frac{\sqrt{10}}{2}}=\frac{3}{\frac{3\sqrt{10}}{2}}$��
��OE=1��
��MP��x�ᣬ
��$\frac{3-t}{3}=\frac{PN}{1}$��
���PN=1-$\frac{t}{3}$��
��d=MN-PN=6-2t-��1-$\frac{t}{3}$��=-$\frac{5}{3}t+5$��
��AO=3����P��0��t��ΪAO��һ�㣬
��0��t��3��
��d=-$\frac{5}{3}t+5$��0��t��3����
��3����ͼ2��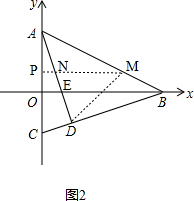
��MP��x�ᣬ
��$\frac{AN}{AE}=\frac{AP}{AO}$��
��$\frac{AN}{\sqrt{{3}^{2}{+1}^{2}}}=\frac{AN}{\sqrt{10}}=\frac{3-t}{3}$��
��AN=$\frac{\sqrt{10}}{3}��3-t��$��
��DN=AD-AN=$\frac{3\sqrt{10}}{2}$-$\frac{\sqrt{10}}{3}��3-t��$=$\frac{\sqrt{10}}{3}t+\frac{\sqrt{10}}{2}$��
��MP��x�ᣬ
��$\frac{AM}{AB}=\frac{AP}{AO}$��
��$\frac{AM}{\sqrt{{6}^{2}{+3}^{2}}}=\frac{3-t}{3}$��
���AM=$\sqrt{5}$��3-t����
�֡�AD=$\frac{3\sqrt{10}}{2}$����DAM=90��-45��=45�㣬
��DM2=AD2+AM2-2AD•AM•cos45��
=${��\frac{3\sqrt{10}}{2}��}^{2}$+${[\sqrt{5}��3-t��]}^{2}$-2��$\frac{3\sqrt{10}}{2}$��$\sqrt{5}$��3-t����$\frac{\sqrt{2}}{2}$
=$\frac{45}{2}$+5t2-30t+45-45+15t
=$\frac{45}{2}$+5t2-15t
�ٵ���MND�ǵ��������Σ���DM=DNʱ��
$\frac{45}{2}$+5t2-15t=${��\frac{\sqrt{10}}{3}t+\frac{\sqrt{10}}{2}��}^{2}$��
�������ɵ�
7t2-33t+36=0��
���t=$\frac{12}{7}$��t=3��
��0��t��3��
��t=$\frac{12}{7}$��
�ڵ���MND�ǵ��������Σ���DM=MNʱ��
$\frac{45}{2}$+5t2-15t=${��-\frac{5}{3}t+5��}^{2}$��
�������ɵ�
8t2+6t-9=0��
���t=$\frac{3}{4}$��t=-$\frac{3}{2}$��
��0��t��3��
��t=$\frac{3}{4}$��
���ϣ��ɵ�
����MND����DMΪ���ĵ���������ʱ��t=$\frac{12}{7}$��t=$\frac{3}{4}$��
���� ��1��������Ҫ������һ�κ����ۺ��⣬�����˷������������������˷�������˼���Ӧ�ã����������ν��˼���Ӧ�ã������˴���֪����ͼ���л�ȡ��Ϣ���������û�ȡ����Ϣ�����Ӧ�������������
��2��������������������Ƶ��ж������ʵ�Ӧ�ã�Ҫ�������գ�������Ĺؼ���Ҫ��ȷ�������߷��������Ӧ�ߵı���ȵ��������������ƣ���������нǷ��������Ӧ�ߵı�����ҼнǶ�Ӧ��ȵ��������������ƣ������Ƿ���������Ƕ�Ӧ��ȵ��������������ƣ�
��3����������˵��������ε����ʺ�Ӧ�ã�Ҫ�������գ�������Ĺؼ���Ҫ��ȷ���ٵ��������ε�������ȣ��ڵ��������ε���������ȣ��۵��������εĶ���ƽ���ߡ��ױ��ϵ����ߡ��ױ��ϵĸ���غϣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������������ͬһ��O�������ֱ�����������ʻ10km������A��B���������ǵ���ʻ·����ͬ�����ǵ���ʻ·����ͬ��
��ͼ������������ͬһ��O�������ֱ�����������ʻ10km������A��B���������ǵ���ʻ·����ͬ�����ǵ���ʻ·����ͬ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
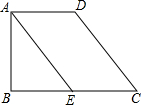 ��ͼ���ı���ABCD�У�AD��BC��AE��DC����EΪ��BC���е㣬����AB=4��AD=3��CD=5�����ı���ABCD�������
��ͼ���ı���ABCD�У�AD��BC��AE��DC����EΪ��BC���е㣬����AB=4��AD=3��CD=5�����ı���ABCD��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
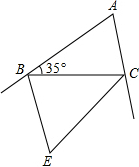 ��ͼ��BE��CE�ֱ��ǡ�ABC���������ƽ���ߣ��ҽ��ڵ�E����A=80�㣬
��ͼ��BE��CE�ֱ��ǡ�ABC���������ƽ���ߣ��ҽ��ڵ�E����A=80�㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com