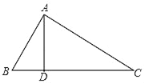
【题目】题目：如图，在△ABC中，点D是BC边上一点，连结AD，若AB＝10，AC＝17，BD＝6，AD＝8，解答下列问题：
（1）求∠ADB的度数；
（2）求BC的长．
小强做第（1）题的步骤如下：∵AB2＝BD2+AD2
∴△ABD是直角三角形，∠ADB＝90°．
（1）小强解答第（1）题的过程是否完整，如果不完整，请写出第（1）题完整的解答过程
（2）完成第（2）题．
考前必练系列答案科目：初中数学 来源： 题型：
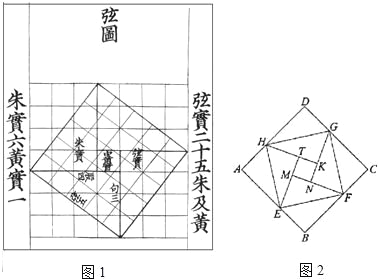
【题目】我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到，它是由八个全等的直角三角形拼接而成．记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，若S1+S2+S3=10，则S2的值是_________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．
（1）在图1中证明CE=CF；
（2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；
（3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，为了测量山顶铁塔AE的高，小明在27m高的楼CD底部D测得塔顶A的仰角为45°，在楼顶C测得塔顶A的仰角36°52′．已知山高BE为56m，楼的底部D与山脚在同一水平线上，求该铁塔的高AE．（参考数据：sin36°52′≈0.60，tan36°52′≈0.75）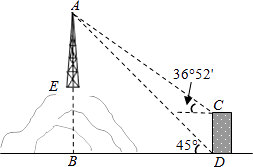
查看答案和解析>>
科目：初中数学 来源： 题型：
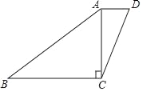
【题目】如图，一张四边形纸片ABCD，AB＝20，BC＝16，CD＝13，AD＝5，对角线AC⊥BC．
（1）求AC的长；
（2）求四边形纸片ABCD的面积；
（3）若将四边形纸片ABCD沿AC剪开，拼成一个与四边形纸片ABCD面积相等的三角形，直接写出拼得的三角形各边高的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将下列各数填入相应的集合内：
3.1415926，﹣2.1，|﹣
|， 0， 
， -2.626626662…，
， 
．
正数集合：{ …}
负数集合：{ …}
有理数集合：{ …}
无理数集合：{ …}．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一架2.5米长的梯子AB 斜靠在一座建筑物上，梯子底部与建筑物距离BC 为0.7米.
（1）求梯子上端A到建筑物的底端C的距离（即AC的长）；
（2）如果梯子的顶端A沿建筑物的墙下滑0.4米（即AA′=0.4米），则梯脚B将外移（即BB′的长）多少米？
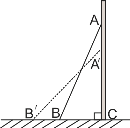
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
