
【题目】小明家需要用钢管做防盗窗,按设计要求,其中需要长为 0.8m,2.5m 且粗细相同的钢管分别为 100 根,32 根,并要求这些用料不能是焊接而成的.现钢材市场的这种规格的钢管每根为 6m.
(1)试问一根 6 米长的钢管有哪些裁剪方法呢?请填写下空(余料作废).
方法 1:当只裁剪长为 0.8 米的用料时,最多可剪 根;
方法 2:当先剪下 1 根 2.5 米的用料时,余下部分最多能剪 0.8 米长的用料 根:
方法 3:当先剪下 2 根 2.5 米的用料时,余下部分最多能剪 0.8 米长的用料 根.
(2)联合用(1)中的方法 2 和方法 3 各裁剪多少根 6 米长的钢管,才能刚好得到所需要的相应数量的材料?
(3)小明经过探究发现:如果联合(1)中的二种或三种裁剪方法,还有多种方案能刚好得 到所需要的相应数量的材料,并且所需要 6m 长的钢管与(2)中根数相同,试帮小明说明理由,并写出一种与(2)不同的裁剪方案.
【答案】(1)7,4,1;(2)用方法二剪 24 根,方法三裁剪 4 根 6m 长的钢管;(3)方法一与方法三联合,所需要 6m 长的钢管与(2)中根数相同.
【解析】(1)由总数÷每份数=分数就可以直接得出结论;
(2)设用方法②剪x根,方法③裁剪y根6m长的钢管,就有x+2y=32,4x+y=100,由此方程构成方程组求出其解即可.
(3)设方法①裁剪m根,方法③裁剪n根6m长的钢管和设方法①裁剪a根,方法②裁剪b根6m长的钢管,分别建立方程组求出其解即可.
(1)①6÷0.8=7…0.4,因此当只裁剪长为0.8m的用料时,最多可剪7根;
②(6-2.5)÷0.8=4…0.3,因此当先剪下1根2.5m的用料时,余下部分最多能剪0.8m长的用料4根;
③(6-2.5×2)÷0.8=1…0.2,因此当先剪下2根2.5m的用料时,余下部分最多能剪0.8m长的用料1根;
(2)设用方法②剪x根,方法③裁剪y根6m长的钢管,由题意,得
![]() ,
,
解得:![]() .
.
答:用方法②剪24根,方法③裁剪4根6m长的钢管;
(3)设方法①裁剪m根,方法③裁剪n根6m长的钢管,由题意,得
![]() ,
,
解得:![]() ,
,
∴m+n=28.
∵x+y=24+4=28,
∴m+n=x+y.
设方法①裁剪a根,方法②裁剪b根6m长的钢管,由题意,得
![]() ,
,
解得:![]() 无意义.
无意义.
∴方法①与方法③联合,所需要6m长的钢管与(2)中根数相同.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ![]() ),点C的坐标为(
),点C的坐标为(![]() ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
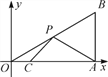
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程kx2﹣(3k﹣1)x+2(k﹣1)=0
(1)求证:无论k为任何实数,方程总有实数根;
(2)若此方程有两个实数根x1 , x2 , 且|x1﹣x2|=2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一条直线与反比例函数y= ![]() (x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=
(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y= ![]() (x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为( )
(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为( ) 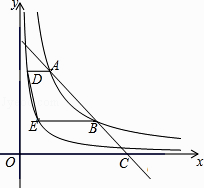
A.4
B.![]()
C.5
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
(1)利用图1,求证:四边形ABCD是菱形. 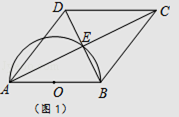
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8. ①连结OE,求△OBE的面积.
②求扇形AOE的面积.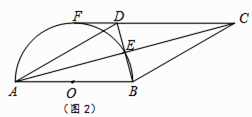
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】特值验证:
当![]() ,0,1,2,5,…时,计算代数式
,0,1,2,5,…时,计算代数式![]() 的值,分别得到5,2,1,2,17,….当x的取值发生变化时,代数式
的值,分别得到5,2,1,2,17,….当x的取值发生变化时,代数式![]() 的值却有一个确定的范围,通过多次验证可以发现它的值总大于或等于1,所以1就是它的最小值.
的值却有一个确定的范围,通过多次验证可以发现它的值总大于或等于1,所以1就是它的最小值.
变式求证:
我们可以用学过的知识,对![]() 进行恒等变形:
进行恒等变形:![]() .(注:这种变形方法可称为“配方”)
.(注:这种变形方法可称为“配方”) ![]() ,
,![]() .所以无论x取何值,代数式
.所以无论x取何值,代数式![]() 的值不小于1,即最小值为1.
的值不小于1,即最小值为1.
迁移实证:
(1)请你用“配方”的方法,确定![]() 的最小值为3;
的最小值为3;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com