
【题目】如图,△ABC中,AB=AC, ,∠C==30°,DA⊥BA于点A,BC=16cm, 则AD=__.

【答案】![]()
【解析】
根据等边对等角可得∠B=∠C,再利用三角形的内角和定理求出∠BAC=120°,然后求出∠CAD=30°,从而得到∠CAD=∠C,根据等角对等边可得AD=CD,再根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2AD,然后根据BC=BD+CD列出方程求解即可.
解:∵AB=AC,
∴∠B=∠C=30°,
∴∠BAC=180°-2×30°=120°,
∵DA⊥BA,
∴∠BAD=90°,
∴∠CAD=120°-90°=30°,
∴∠CAD=∠C,
∴AD=CD,
在Rt△ABD中,∵∠B=30°,∠BAD=90°,
∴BD=2AD,
∴BC=BD+CD=2AD+AD=3AD,
∵BC=16cm,
∴AD=![]() cm.
cm.


科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD的对角线AC,BD相交于点O,给出下列4个条件:①AB∥CD;②OA=OC;③AB=CD;④AD∥BC.从中任取两个条件,能推出四边形ABCD是平行四边形的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.
甲:线段AF与线段CD的长度总相等;
乙:直线AF和直线CD所夹的锐角的度数不变.
那么,你认为( )

A. 甲、乙都对 B. 乙对甲不对 C. 甲对乙不对 D. 甲、乙都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
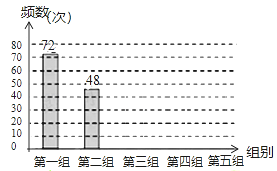
【题目】某网络约车公司近期推出了”520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5000个“单次营运里程”数据,这些里程数据均不超过25(公里),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图(如图).
组别 | 单次营运里程“x“(公里) | 频数 |
第一组 | 0<x≤5 | 72 |
第二组 | 5<x≤10 | a |
第三组 | 10<x≤15 | 26 |
第四组 | 15<x≤20 | 24 |
第五组 | 20<x≤25 | 30 |
根据统计表、图提供的信息,解答下面的问题:
(1)①表中a= ;②样本中“单次营运里程”不超过15公里的频率为 ;③请把频数分布直方图补充完整;
(2)请估计该公司这5000个“单次营运里程”超过20公里的次数;
(3)为缓解城市交通压力,维护交通秩序,来自某市区的4名网约车司机(3男1女)成立了“交通秩序维护”志愿小分队,若从该小分队中任意抽取两名司机在某一路口维护交通秩序,请用列举法(画树状图或列表)求出恰好抽到“一男一女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,回答问题:
解方程![]() ,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设![]() ,那么
,那么![]() ,于是原方程可变为
,于是原方程可变为![]() ①,解得
①,解得![]() ,
,![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
∴原方程有四个根:![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 在由原方程得到方程①的过程中,利用________法达到________的目的,体现了数学的转化思想.
在由原方程得到方程①的过程中,利用________法达到________的目的,体现了数学的转化思想.
![]() 解方程
解方程![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC (BC>AD),∠D=90°,∠ABE=45°,BC=CD,
若AE=5,CE=2,则BC的长度为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左边到右边的变形,是因式分解的是( )
A.y![]() ﹣5y﹣6=(y﹣6)(y+1)B.a
﹣5y﹣6=(y﹣6)(y+1)B.a![]() +4a﹣3=a(a+4)﹣3
+4a﹣3=a(a+4)﹣3
C.x(x﹣1)=x![]() ﹣xD.m
﹣xD.m![]() +n
+n![]() =(m+n)(m﹣n)
=(m+n)(m﹣n)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com