
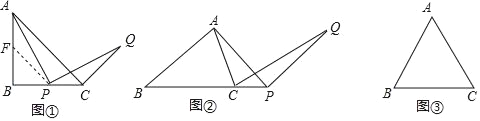
【题目】在△ABC中,BA=BC,∠ABC=α(0°<α<180°),点P为直线BC上一动点(不与点B,C重合),连接AP,将线段PA绕点P顺时针旋转α度得到线段PQ,连接CQ.
(1)当α=90°,且点P在线段BC上时,过P作PF∥AC交直线AB于点F,如图1,图中与△APF全等的是哪个三角形,∠ACQ的度数.
(2)当点P在BC延长线上,AB:AC=m:n时,如图2,试求线段BP与CQ的比值;
(3)当点P在直线BC上,α=60°,∠APB=30°,CP=4时,请直接写出线段CQ的长.
【答案】(1)△PQC,90;(2)![]() ;(3)线段CQ的长为2或8.
;(3)线段CQ的长为2或8.
【解析】
(1)依据条件判定△APF≌△PQC,可得∠PCQ=∠AFP=135°,依据∠ACB=45°,可得∠ACQ=90°;
(2)过P作PF∥AC,交BA的延长线于F,判定△AFP≌△PCQ,可得FP=CQ,再根据△ABC∽△FBP,可得![]() ,进而得出
,进而得出![]() ;
;
(3)分两种情况进行讨论:点P在CB的延长线上,点P在BC的延长线上,分别依据全等三角形的性质以及含30°角的直角三角形的性质,即可得到线段CQ的长.
(1)如图①,∵∠ABC=90°,AB=CB,
∴△ABC是等腰直角三角形,
∵PF∥AC,
∴∠BPF=∠BFP=45°,
∴△BPF是等腰直角三角形,
∴BF=BP,
∴AF=CP,
由旋转可得,AP=PQ,∠APQ=90°,而∠BPF=45°,
∴∠QPC=45°﹣∠APF,
又∵∠PAF=∠PFB﹣∠APF=45°﹣∠APF,
∴∠PAF=∠QPC,
∴△APF≌△PQC(SAS)
∴∠PCQ=∠AFP=135°,
又∵∠ACB=45°,
∴∠ACQ=90°,
故答案为:△PQC,90;
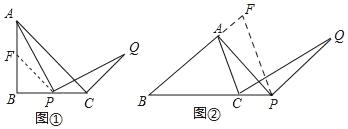
(2)如图②,过P作PF∥AC,交BA的延长线于F,则![]() ,
,
又∵AB=BC,
∴AF=CP,
又∵∠FAP=∠ABC+∠APB=α+∠APB,∠CPQ=∠APQ+∠APB=α+∠APB,
∴∠FAP=∠CPQ,
由旋转可得,PA=PQ,
∴△AFP≌△PCQ(SAS),
∴FP=CQ,
∵PF∥AC,
∴△ABC∽△FBP,
∴![]()
∴![]() ;
;
(3)如图,当P在CB的延长线上时,
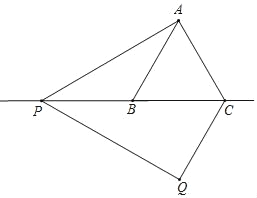
∵∠CPQ=∠APQ﹣∠APB=60°﹣30°=30°,
∴∠APC=∠QPC,
又∵AP=QP,PC=PC,
∴△APC≌△QPC(SAS),
∴CQ=AC,
又∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠ABC=60°,∠BAP=∠ABC﹣∠APB=30°,
∴BP=AB=BC=![]() PC=2,
PC=2,
∴QC=AC=BC=2;
如图,当P在BC的延长线上时,连接AQ,
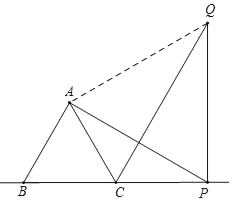
由旋转可得,AP=QP,∠APQ=∠ABC=60°,
∴△APQ是等边三角形,
∴AQ=PQ,∠APQ=60°=∠AQP,
又∵∠APB=30°,∠ACB=60°,
∴∠CAP=30°,∠CPQ=90°,
∴∠CAP=∠APA,
∴AC=PC,且AQ=PQ,CQ=CQ
∴△ACQ≌△PCQ(SSS)
∴∠AQC=∠PQC=![]() ∠AQP=30°,
∠AQP=30°,
∴Rt△PCQ中,CQ=2CP=8.
综上所述,线段CQ的长为2或8.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1=![]() 与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
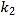
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() x+b的解.
x+b的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2,并指出她与嘉嘉抽到勾股数的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段BC长为13,以C为顶点,CB为一边的∠α满足cosα=![]() .锐角△ABC的顶点A落在∠α的另一边上,且满足sinA=
.锐角△ABC的顶点A落在∠α的另一边上,且满足sinA=![]() .求△ABC的高BD及AB边的长,并结合你的计算过程画出高BD及AB边.(图中提供的单位长度供补全图形使用)
.求△ABC的高BD及AB边的长,并结合你的计算过程画出高BD及AB边.(图中提供的单位长度供补全图形使用)
查看答案和解析>>
科目:初中数学 来源: 题型:
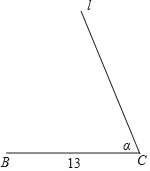
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
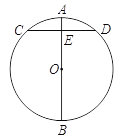
【题目】最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
A. 91.1 B. 91.3 C. 58.2 D. 58.4
查看答案和解析>>
科目:初中数学 来源: 题型:
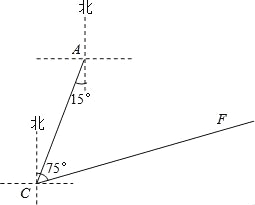
【题目】中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?
说明理由.(![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
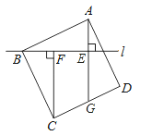
【题目】如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
(1)求证:△ABE≌△BCF;
(2)若∠CBF=65°,求∠AGC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com