
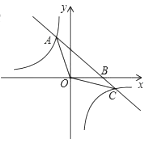
ЁОЬтФПЁПвЛДЮКЏЪ§y1ЃНkx+1Љ2kЃЈkЁй0ЃЉЕФЭМЯѓМЧзїG1ЃЌвЛДЮКЏЪ§y2ЃН2x+3ЃЈЉ1ЃМxЃМ2ЃЉЕФЭМЯѓМЧзїG2ЃЌЖдгкетСНИіЭМЯѓЃЌгавдЯТМИжжЫЕЗЈЃК
ЂйЕБG1гыG2гаЙЋЙВЕуЪБЃЌy1ЫцxдіДѓЖјМѕаЁЃЛ
ЂкЕБG1гыG2УЛгаЙЋЙВЕуЪБЃЌy1ЫцxдіДѓЖјдіДѓЃЛ
ЂлЕБkЃН2ЪБЃЌG1гыG2ЦНааЃЌЧвЦНааЯпжЎМфЕФОрРыЮЊ![]() ЃЎ
ЃЎ
ЯТСабЁЯюжаЃЌУшЪізМШЗЕФЪЧЃЈЁЁЁЁЃЉ
A.ЂйЂке§ШЗЃЌЂлДэЮѓB.ЂйЂле§ШЗЃЌЂкДэЮѓ
C.ЂкЂле§ШЗЃЌЂйДэЮѓD.ЂйЂкЂлЖМе§ШЗ
ЁОД№АИЁПD
ЁОНтЮіЁП
ЛЭМЃЌевГіG2ЕФСйНчЕуЃЌвдМАG1ЕФСйНчжБЯпЃЌЗжЮіГіG1Й§ЖЈЕуЃЌИљОнkЕФе§ИКгыКЏЪ§діМѕБфЛЏЕФЙиЯЕЃЌНсКЯКЏЪ§ЭМЯѓж№ИібЁЯюЗжЮіМДПЩНтД№ЃЎ
НтЃКвЛДЮКЏЪ§y2ЃН2x+3ЃЈЉ1ЃМxЃМ2ЃЉЕФКЏЪ§жЕЫцxЕФдіДѓЖјдіДѓЃЌШчЭМЫљЪОЃЌ

NЃЈЉ1ЃЌ2ЃЉЃЌQЃЈ2ЃЌ7ЃЉЮЊG2ЕФСНИіСйНчЕуЃЌ
взжЊвЛДЮКЏЪ§y1ЃНkx+1Љ2kЃЈkЁй0ЃЉЕФЭМЯѓЙ§ЖЈЕуMЃЈ2ЃЌ1ЃЉЃЌ
жБЯпMNгыжБЯпMQЮЊG1гыG2гаЙЋЙВЕуЕФСНЬѕСйНчжБЯпЃЌДгЖјЕБG1гыG2гаЙЋЙВЕуЪБЃЌy1ЫцxдіДѓЖјМѕаЁЃЛЙЪЂйе§ШЗЃЛ
ЕБG1гыG2УЛгаЙЋЙВЕуЪБЃЌЗжШ§жжЧщПіЃК
вЛЪЧжБЯпMNЃЌЕЋДЫЪБkЃН0ЃЌВЛЗћКЯвЊЧѓЃЛ
ЖўЪЧжБЯпMQЃЌЕЋДЫЪБkВЛДцдкЃЌгывЛДЮКЏЪ§ЖЈвхВЛЗћЃЌЙЪMQВЛЗћКЯЬтвтЃЛ
Ш§ЪЧЕБkЃО0ЪБЃЌДЫЪБy1ЫцxдіДѓЖјдіДѓЃЌЗћКЯЬтвтЃЌЙЪЂке§ШЗЃЛ
ЕБkЃН2ЪБЃЌG1гыG2ЦНаае§ШЗЃЌЙ§ЕуMзїMPЁЭNQЃЌдђMNЃН3ЃЌгЩy2ЃН2x+3ЃЌЧвMNЁЮxжсЃЌПЩжЊЃЌtanЁЯPNMЃН2ЃЌ
ЁрPMЃН2PNЃЌ
гЩЙДЙЩЖЈРэЕУЃКPN2+PM2ЃНMN2
ЁрЃЈ2PNЃЉ2+ЃЈPNЃЉ2ЃН9ЃЌ
ЁрPNЃН![]() ЃЌ
ЃЌ
ЁрPMЃН![]() .
.
ЙЪЂле§ШЗЃЎ
злЩЯЃЌЙЪбЁЃКDЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛЫвТжДЌДгЮЛгкЕЦЫўCЕФББЦЋЖЋ60ЁуЗНЯђЃЌОрРыЕЦЫў60 n mileЕФаЁЕКAГіЗЂЃЌбие§ФЯЗНЯђКНаавЛЖЮЪБМфКѓЃЌЕНДяЮЛгкЕЦЫўCЕФФЯЦЋЖЋ45ЁуЗНЯђЩЯЕФBДІЃЌетЪБТжДЌBгыаЁЕКAЕФОрРыЪЧ( )

A.![]() n mileB.60 n mileC.120 n mileD.
n mileB.60 n mileC.120 n mileD.![]() n mile
n mile
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
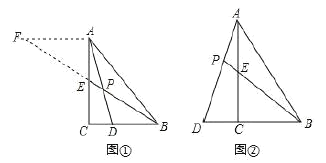
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯЕФжаЯпЃЌЕу
БпЩЯЕФжаЯпЃЌЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯ.
ЩЯ.
ВТЯы:ШчЭМЂйЃЌЕу![]() дк
дк![]() БпЩЯЃЌ
БпЩЯЃЌ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌНЛ
ЃЌНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЮЊ .
ЕФжЕЮЊ .
ЬНОП:ШчЭМЂкЃЌЕу![]() дк
дк![]() ЕФбгГЄЯпЩЯЃЌ
ЕФбгГЄЯпЩЯЃЌ![]() гы
гы![]() ЕФбгГЄЯпНЛгкЕу
ЕФбгГЄЯпНЛгкЕу![]() ЃЌ
ЃЌ ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
гІгУ:дкЬНОПЕФЬѕМўЯТЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() ЕФЖЅЕуЮЊ
ЕФЖЅЕуЮЊ![]() ЃЌгы
ЃЌгы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() ЃЌЖдГЦжсЮЊжБЯп
ЃЌЖдГЦжсЮЊжБЯп![]() ЃЌЕу
ЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФжаЕу.
ЕФжаЕу.
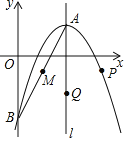
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉаДГіЕу![]() ЕФзјБъВЂЧѓжБЯп
ЕФзјБъВЂЧѓжБЯп![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ3ЃЉЩшЖЏЕу![]() ЃЌ
ЃЌ![]() ЗжБ№дкХзЮяЯпКЭЖдГЦжсlЩЯЃЌЕБвд
ЗжБ№дкХзЮяЯпКЭЖдГЦжсlЩЯЃЌЕБвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЧѓ
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЧѓ![]() ЃЌ
ЃЌ![]() СНЕуЕФзјБъ.
СНЕуЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
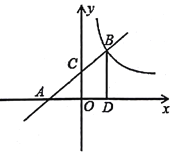
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЧвгыЗДБШР§КЏЪ§
ЃЌЧвгыЗДБШР§КЏЪ§![]() дкЕквЛЯѓЯоФкЕФЭМЯѓНЛгкЕу
дкЕквЛЯѓЯоФкЕФЭМЯѓНЛгкЕу![]() ЃЌзї
ЃЌзї![]() жсгкЕу
жсгкЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжБЯп![]() ЕФКЏЪ§НтЮіЪНЃЛ
ЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕу![]() ЪЧ
ЪЧ![]() жсЩЯЕФЕуЃЌШє
жсЩЯЕФЕуЃЌШє![]() ЕФУцЛ§ЕШгк6ЃЌжБНгаДГіЕу
ЕФУцЛ§ЕШгк6ЃЌжБНгаДГіЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЩш![]() ЕуЪЧ
ЕуЪЧ![]() жсЩЯЕФЕуЃЌЧв
жсЩЯЕФЕуЃЌЧв![]() ЮЊЕШбќШ§НЧаЮЃЌЧѓ
ЮЊЕШбќШ§НЧаЮЃЌЧѓ![]() ЕуЕФзјБъЃЎ
ЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
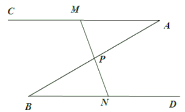
ЁОЬтФПЁПШчЭМЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() жаЕуЃЌЕу
жаЕуЃЌЕу![]() ЮЊЩфЯп
ЮЊЩфЯп![]() ЩЯЃЈВЛгыЕу
ЩЯЃЈВЛгыЕу![]() жиКЯЃЉЕФШЮвтвЛЕуЃЌСЌНг
жиКЯЃЉЕФШЮвтвЛЕуЃЌСЌНг![]() ЃЌВЂЪЙ
ЃЌВЂЪЙ![]() ЕФбгГЄЯпНЛЩфЯп
ЕФбгГЄЯпНЛЩфЯп![]() гкЕу
гкЕу![]() ЃЌЩш
ЃЌЩш![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ3ЃЉЕБ![]() ЕФЭтаФВЛдкШ§НЧаЮЭтВПЪБЃЌЧыжБНгаДГі
ЕФЭтаФВЛдкШ§НЧаЮЭтВПЪБЃЌЧыжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊвЛДЮКЏЪ§![]() гыЗДБШР§КЏЪ§
гыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЯрНЛгкЕу
ЕФЭМЯѓЯрНЛгкЕу![]() гыЕу
гыЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНМА![]() ЕузјБъЃЎ
ЕузјБъЃЎ
ЃЈ2ЃЉИљОнЭМЯѓЛиД№ЃЌдкЪВУДЗЖЮЇЪБЃЌвЛДЮКЏЪ§ЕФжЕДѓгкЗДБШР§КЏЪ§ЕФжЕЃЎ
ЃЈ3ЃЉЧѓШ§НЧаЮ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЎХзЮяЯпy=Љx2+4x+3гыyжсНЛгкЕуAЃЌХзЮяЯпЕФЖдГЦжсгыxжсНЛгкЕуBЃЌСЌНгABЃЌНЋЁїOABШЦзХЕуBЫГЪБеыа§зЊЕУЕНЁїO'A'BЃЎ
ЃЈ1ЃЉгУХфЗНЗЈЧѓХзЮяЯпЕФЖдГЦжсВЂжБНгаДГіAЃЌBСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕБЕуA'ЕквЛДЮТфдкХзЮяЯпЩЯЪБЃЌЁЯO'BO=nЁЯOABЃЌЧыжБНгаДГіnЕФжЕЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕБЁїOABШЦзХЕуBЫГЪБеыа§зЊ60ЁуЃЌжБЯпA'O'НЛxжсгкЕуMЃЌЧѓЁїA'MBЕФУцЛ§ЃЛ
ЃЈ4ЃЉдка§зЊЙ§ГЬжаЃЌСЌНгOO'ЃЌЕБЁЯO'OB=ЁЯOABЪБЃЎжБЯпA'O'ЕФКЏЪ§БэДяЪНЪЧЁЁЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЎдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЮЛЯпЃЌСЌНс
ЕФжаЮЛЯпЃЌСЌНс![]() ЃЌЕу
ЃЌЕу![]() ЪЧБп
ЪЧБп![]() ЩЯЕФвЛИіЖЏЕуЃЌСЌНс
ЩЯЕФвЛИіЖЏЕуЃЌСЌНс![]() НЛ
НЛ![]() гк
гк![]() ЃЌНЛ
ЃЌНЛ![]() гк
гк![]() ЃЎ
ЃЎ
(1)ЕБЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЪБЃЌЧѓ
ЕФжаЕуЪБЃЌЧѓ![]() ЕФжЕМА
ЕФжЕМА![]() ЕФГЄ
ЕФГЄ
(2) ЕБЫФБпаЮ![]() гыЫФБпаЮ
гыЫФБпаЮ![]() ЕФУцЛ§ЯрЕШЪБЃЌЧѓ
ЕФУцЛ§ЯрЕШЪБЃЌЧѓ![]() ЕФГЄЃК
ЕФГЄЃК
(3)ШчЭМ2ЃЎвд![]() ЮЊжБОЖзї
ЮЊжБОЖзї![]() ЃЎ
ЃЎ
ЂйЕБ![]() е§КУОЙ§Еу
е§КУОЙ§Еу![]() ЪБЃЌЧѓжЄЃК
ЪБЃЌЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃК
ЕФЧаЯпЃК
ЂкЕБ![]() ЕФжЕТњзуЪВУДЬѕМўЪБЃЌ
ЕФжЕТњзуЪВУДЬѕМўЪБЃЌ![]() гыЯпЖЮ
гыЯпЖЮ![]() гаЧвжЛгавЛИіНЛЕуЃЎ
гаЧвжЛгавЛИіНЛЕуЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com