
分析 审题可知这是一道含有字母系数的二次方程组,首先代入消元得到含有字母a的一元二次方程:x2+2ax+12a2-5=0,用公式法求出方程的根-a±$\sqrt{5-11{a}^{2}}$:利用判别式分析得出a<$\frac{8}{11}$,再根据“解为正整数,y-x=6a”得出6a为整数,a的绝对值只能取值为:$\frac{2}{3}$,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$,最后代入根的公式,根据解为正整数进行检验.
解答 解:
方程组消元得:x2+2ax+12a2-5=0
用公式法求得方程的根为:x=-a±$\sqrt{5-11{a}^{2}}$,由△=-44a2+20≥0,得出|a|≤$\sqrt{\frac{5}{11}}$,
由x和y都是正整数知y-x=6a为整数,所以|a|的可能值为:$\frac{2}{3}$,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$
把a的值代入求根公式计算:当a=$\frac{1}{2}$时,x=-a±$\sqrt{5-11{a}^{2}}$,x=1(满足题意)或x=-2(舍去)
当a=$\frac{1}{6}$时,x=-a±$\sqrt{5-11{a}^{2}}$,x=2(满足题意)或x=$-\frac{7}{3}$(舍去)
依次验证得出:只有$\frac{1}{2}$和$\frac{1}{6}$满足题意.
故答案为:$\frac{1}{2}$,$\frac{1}{6}$.
点评 此题主要考查了方程组的消元法,以及对于一元二次方程的根的探索研究,在解决此题时,认真分析,分别讨论是关键,做题一定不要漏解.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:解答题
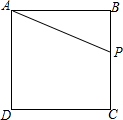 如图所示,正方形ABCD的边长为5,P为BC上一动点(不与B、C两点重合),若CP=x,△ABP的面积为y,求出y与x之间的函数关系式,并写出自变量x的取值范围.
如图所示,正方形ABCD的边长为5,P为BC上一动点(不与B、C两点重合),若CP=x,△ABP的面积为y,求出y与x之间的函数关系式,并写出自变量x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com