
【题目】如图,⊙C经过原点且与两坐标轴分别交于点A与点B,点A的坐标为(0,8),M是劣弧BO上任一点,∠BMO=120°,求:
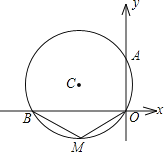
(1)⊙C的半径;
(2)圆心C的坐标.
【答案】(1)圆的半径为8;(2)点C的坐标为![]() .
.
【解析】
(1)连接AB,由于∠AOB是直角,根据圆周角定理可知AB必为⊙C的直径,即C是AB的中点,已知A点坐标,关键是求出B点的坐标.由图知:四边形ABMO是圆的内接四边形,因此内对角∠BAO、∠BMO互补,由此求得∠BAO的度数,进而可在Rt△BAO中,根据直角三角形的性质得到OB的长,从而确定点B的坐标,由此得解.
(2)作CD⊥OB于点D,利用垂径定理以及解直角三角形求得BD的长,从而求得答案,
(1)解:连接AB,过点C作CD⊥OB于点D,
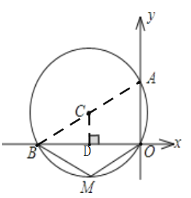
∴OD=BD,
∵∠AOB=90°
∴AB是圆O的直径,
∵四边形AOMB是圆C的内接四边形,
∴∠BAO+∠BMO=180°
∴∠BAO=180°-120°=60°
∴∠ABO=90°-60°=30°
∴AB=2OA=2×8=16,
∴圆的半径为8.
(2)解: 在Rt△CDB中,∠CBD=30°,CB=4
∴CD=8÷2=4,
BD=OD=CBcos∠CBD=![]()
∴点C的坐标为![]()


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度![]() 得到△AED,点B、C的对应点分别是E、D.
得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若![]() =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,两个三角形的顶点都在格点(网线的交点)上,下列方案中不能把△ABC平移至△DEF位置的是( )
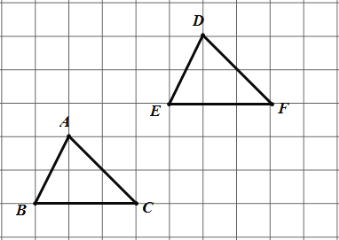
A.先把△ABC沿水平方向向右平移4个单位长度,再向上平移3个单位长度
B.先把△ABC向上平移3个单位长度,再沿水平方向向右平移4个单位长度
C.把△ABC沿BE方向移动5个单位长度
D.把△ABC沿BE方向移动6个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
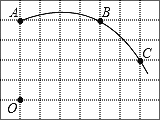
(1)请完成如下操作:
①以点O为坐标原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,只借助直尺确定该圆弧所在圆的圆心D,并连接AD、CD.(保留作图痕迹,不写作法)
(2)请在(1)的基础上,完成下列填空与计算:
①写出点的坐标:C 、D ;
②⊙D的半径= ;(结果保留根号)
③求扇形ADC的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工程上常用钢珠来测量零件上小孔的直径.假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,如图所示,则这个小孔的直径AB是_________毫米.
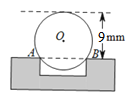
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,FE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=![]() ;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为
;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为![]() ,其中正确的是( )
,其中正确的是( )
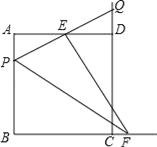
A. ①② B. ①②④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,设二次函数y=ax2﹣4ax,其中为常数且a<0.
(1)若函数y=ax2﹣4ax的图象经过点(2,4),求此函数表达式;
(2)若抛物线y=ax2﹣4ax的顶点在双曲线![]() 上,试说明k的符号;
上,试说明k的符号;
(3)已知(m,y1)、(m+1,y2)、(m+2,y3),(0<m<1)都是抛物线y=ax2﹣4ax(a<0)上的点,请判断y1,y2,y3的大小,并说明理由﹒
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com