
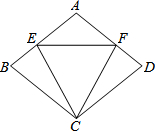
 如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等.
如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等.分析 (1)根据等腰三角形的性质和菱形的性质证得∠B=∠D,∠CEB=∠CFD,CE=CF就可以证明结论成立;
(2)设∠B=x,根据三角形内角和定理和等腰三角形的性质得到∠BCE=180-2x,∠FCD=180-2x,用x表示出∠BCD,进一步利用菱形的性质得出∠B+∠BCD=180°,联立方程求得答案即可.
解答 (1)证明:∵四边形ABCD是菱形;
∴CB=CD,且∠B=∠D,
∵△CEF等腰三角形,
∴CE=CF,
∵CE=CB,CF=CD
∴∠B=∠CEB,∠D=∠CFD,
∴∠CEB=∠CFD,
$\left\{\begin{array}{l}{∠B=∠D}\\{∠CEB=∠CFD}\\{CE=CF}\end{array}\right.$
∴△BEC≌△DFC(AAS)
(2)解:设∠B=x
∵CE=CB,
∴∠CEB=∠B=x,
∴∠BCE=180-2x,
同理∠FCD=180-2x,
∵△CEF是等边三角形,
∴∠ECF=60°,
∵ABCD是菱形;
∴∠B+∠BCD=180°,
∴x+2(180-2x)+60°=180°,
x=80°,
∴∠B=80°.
点评 此题考查菱形的性质,等腰三角形的性质,三角形全等的判定,以及三角形三角和定理,注意掌握方程思想与数形结合思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
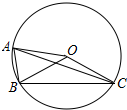 如图,⊙O是△ABC的外接圆,∠BOC=3∠AOB,若∠ACB=20°,则∠BAC的度数是( )
如图,⊙O是△ABC的外接圆,∠BOC=3∠AOB,若∠ACB=20°,则∠BAC的度数是( )| A. | 120° | B. | 80° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
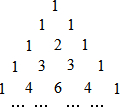 如图所示的“贾宪三角”告诉了我们二项式乘方展开式的系数规律,如:第四行的四个数恰好对应着(a+b)3的展开式a3+3a2b+3ab2+b3的系数; 第五行的五个数恰好对应着(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数;
如图所示的“贾宪三角”告诉了我们二项式乘方展开式的系数规律,如:第四行的四个数恰好对应着(a+b)3的展开式a3+3a2b+3ab2+b3的系数; 第五行的五个数恰好对应着(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
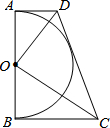 如图,在直角梯形ABCD中AD∥BC.∠ABC=90°DC与以AB为直径的半圆⊙O相切,⊙O的半径为r,在下列结论:①OD⊥OC;②AD+BC=DC; ③S△AOD+S△BOC=S△DOC; ④AD•BC=r2中正确的个数有( )
如图,在直角梯形ABCD中AD∥BC.∠ABC=90°DC与以AB为直径的半圆⊙O相切,⊙O的半径为r,在下列结论:①OD⊥OC;②AD+BC=DC; ③S△AOD+S△BOC=S△DOC; ④AD•BC=r2中正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com