
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() 现有以下四个结论:
现有以下四个结论:
①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积为4;
的面积为4;
④![]() 的面积最大为3.其中正确的结论有( )
的面积最大为3.其中正确的结论有( )

A.①②④B.①②③C.②③④D.①②③④
【答案】B
【解析】
根据等腰三角形的性质、全等三角形的性质、三角形的面积公式可以分别判断出题目中的各个小题是否成立,从而可以解答本题.
解:连接DC,
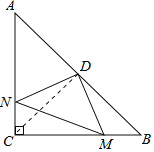
∵在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,
∴CD=![]() AB=AD=BD,CD⊥AB,∠ACD=∠BCD=45°,∠A=∠B=45°,
AB=AD=BD,CD⊥AB,∠ACD=∠BCD=45°,∠A=∠B=45°,
在△CDN和△BDM中,
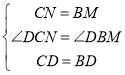 ,
,
∴△CDN≌△BDM(SAS),
∴∠NDC=∠MDB,DN=DM,故①正确,
∵∠CDM+∠MDB=∠CDB=90,
∴∠NDC+∠CDM=90°,
即∠NDM=90°,故②正确,
∵四边形CMDN的面积等于△NDC与△CDM的面积之和,
∴四边形CMDN的面积等于△MDB与△CDM的面积之和,
∴四边形CMDN的面积是:![]() CACB×
CACB×![]() =
=![]() ×4×4×
×4×4×![]() =4,故③正确,
=4,故③正确,
设CM=x,则BM=4![]() x,CN=4
x,CN=4![]() x,
x,
∴△CMN的面积是:![]() ,
,
∵0<x<4,
∴当x=2时,△CMN的面积取得最大值,此时△CMN的面积是2,故④错误;
∴正确的结论有:①②③;
故选:B.


科目:初中数学 来源: 题型:
【题目】老师组织学生做分组摸球实验.给每组准备了完全相同的实验材料,一个不透明的袋子,袋子中装有除颜色外都相同的3个黄球和若干个白球.先把袋子中的球搅匀后,从中随意摸出一个球,记下球的颜色再放回,即为一次摸球.统计各组实验的结果如下:
一组 | 二组 | 三组 | 四组 | 五组 | 六组 | 七组 | 八组 | 九组 | 十组 | |
摸球的次数 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
摸到白球的次数 | 41 | 39 | 40 | 43 | 38 | 39 | 46 | 41 | 42 | 38 |
请你估计袋子中白球的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC、BD交于点O, 自点A作AE⊥BD于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,则BD的长为( )cm.
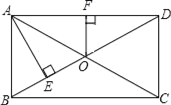
A.6B.9C.12D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法合理的是( )
A. 小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30%
B. 抛掷一枚普通的正六面体骰子,出现6的概率是![]() 的意思是每6次就有1次掷得6
的意思是每6次就有1次掷得6
C. 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖。
D. 在一次课堂进行的试验中,甲、乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做了一个转盘,转盘上的指针一头粗一头细,小明将转盘挂在垂直于地面的墙壁上.

![]() 若将指针固定,转动转盘,则指针细的一头指向红色的概率是多少?
若将指针固定,转动转盘,则指针细的一头指向红色的概率是多少?
![]() 若将转盘固定(如图,红色朝上),转动指针,那么指针细的一头指向红色的概率和第一个问题中的概率一样吗?为什么?
若将转盘固定(如图,红色朝上),转动指针,那么指针细的一头指向红色的概率和第一个问题中的概率一样吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①∠A=2∠BFC﹣180°;②DE﹣BD=CE;③△ADE的周长等于AB与AC的和;④BF>CF.其中正确的有( )

A.①B.①②C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种优质蜜柚,投入市场销售时,经调查,该蜜柚每天销售量y(千克)与销售单价x(元/千克)之间符合一次函数关系,如图所示.

(1)求y与x的函数关系式;
(2)某农户今年共采摘该蜜柚4500千克,其保质期为40天,若以18元/千克销售,问能否在保质期内销售完这批蜜柚?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是( )

A. AE∥BD B. AB=BF C. AF∥CD D. DF=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com