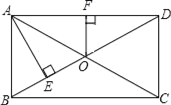
【题目】如图，在矩形ABCD中，对角线AC、BD交于点O， 自点A作AE⊥BD于点E，且BE：ED=1：3，过点O作OF⊥AD于点F，若OF=3cm，则BD的长为（ ）cm．
A.6B.9C.12D.15
【答案】C
【解析】
根据矩形的性质得出AC=BD，BD=2BO=2OD，AC=2AO，∠BAD=90°，求出AO=BO，根据等边三角形的判定得出△ABO是等边三角形，求出∠BAO=60°，∠DAO=30°，即可求出AO，即可求出答案．
∵四边形ABCD是矩形，∴AC=BD，BD=2BO=2OD，AC=2AO，∠BAD=90°，∴AO=BO，
∵BE：ED=1：3，∴BE=EO，
∵AE⊥BD，∴AB=AO，即AO=OB=AB，
∴△ABO是等边三角形，
∴∠BAO=60°，∴∠DAO=90°-60°=30°，
∵OF⊥AD于点F，OF=3cm，∴∠AFO=90°，AO=2OF=6cm，
∴AC=2AO=12cm，∴BD=12cm，故选C．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】一个钢筋三角架三边长分别为
，
，
，现在要做一个和它相似的钢筋三角架，而只有长为
和的两根钢筋，要求以其中的一根为一边，从另一根上截两段（允许有余料）作为另两边，则不同的截法有（ ）
A. 一种 B. 两种 C. 三种 D. 四种或四种以上
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】工人师傅用一块长为10dm，宽为6dm的矩形铁皮制作一个无盖的长方体容器，需要将四角各裁掉一个正方形．（厚度不计）
（1）在图中画出裁剪示意图，用实线表示裁剪线，虚线表示折痕；并求长方体底面面积为12dm2时，裁掉的正方形边长多大？
（2）若要求制作的长方体的底面长不大于底面宽的五倍，并将容器进行防锈处理，侧面每平方分米的费用为0.5元，底面每平方分米的费用为2元，裁掉的正方形边长多大时，总费用最低，最低为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，用四个螺丝将四条不可弯曲的木条围成一个木框，不计螺丝大小，其中相邻两螺丝的距离依次为2、3、4、6，且相邻两木条的夹角均可调整．若调整木条的夹角时不破坏此木框，则任两个螺丝间的距离的最大值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图1，在平面直角坐标系中，一次函数
的图像交x轴于点A，交y轴于点B，点C是点A关于y轴对称的点，过点C作y轴平行的射线CD，交直线AB与点D，点P是射线CD上的一个动点．
（1）求点A、B的坐标．
（2）如图2，将△ACP沿着AP翻折，当点C的对应点E落在直线AB上时，求点P的坐标．
（3）若直线OP与直线AD有交点，不妨设交点为Q（不与点D重合），连接CQ，是否存在点P，使得S△CPQ =2S△DPQ，若存在，请直接写出点P坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平行四边形ABCD的两条对角线相交于O，且AC平分∠DAB．
（1）求证：四边形ABCD是菱形；
（2）若AC=8，BD=6，试求点O到AB的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，
为原点，点
，点
，把
绕点
逆时针旋转，得
，点
、旋转后的对应点为
、
，记旋转角为ɑ．
如图
，若ɑ
，求
的长；
如图
，若ɑ
，求点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，
，点
为
的中点，
，
分别在
，
上，且
现有以下四个结论：
①
；②
；③四边形
的面积为4；
④
的面积最大为3.其中正确的结论有（ ）
A.①②④B.①②③C.②③④D.①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动，每位同学必须且只能选择一项球类运动，对该校学生随机抽取
进行调查，根据调查结果绘制了如下不完整的频数分布表和扇形统计图：
运动项目 | 频数(人数) |
羽毛球 | 30 |
篮球 |
|
乒乓球 | 36 |
排球 |
|
足球 | 12 |
请根据以上图表信息解答下列问题：
(1)频数分布表中的
，
；
(2)在扇形统计图中，“排球”所在的扇形的圆心角为 度；
(3)全校有多少名学生选择参加乒乓球运动？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
