
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在同一条直线上,M,N分别为BE,CD的中点.
(1)求证:△ABE≌ACD;
(2)判断△AMN的形状,并说明理由.

【答案】(1)证明见解析(2)△AMN为等腰三角形;理由见解析
【解析】
(1)由∠BAC=∠DAE,等式左右两边都加上∠CAE,得到一对角相等,再由AB=AC,AD=AE,利用SAS可得出三角形ABE与三角形ACD全等;
(2)由M与N分别为BE,CD的中点,且BE=CD,可得出ME=ND,由△ABE与△ACD全等,对应角∠AEB=∠ADC,利用SAS可得出△AME与△AND全等,利用全等三角形的对应边相等可得出AM=AN,即△AMN为等腰三角形.
(1)∵∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD,
在△ABE和△ACD中,
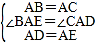 ,
,
∴△ABE≌△ACD(SAS);
(2)∵△ABE≌△ACD
∴BE=CD,∠AEM=∠ADC,
∵M、N分别为BE、CD的中点,
∴ME=ND,
在△AEM和△ADN中,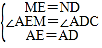 ,
,
∴△AEM≌△ADN(SAS),
∴AM=AN,
即△AMN为等腰三角形.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 碟子的高度(单位:cm) |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
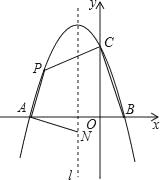
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
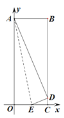
【题目】如图,分别以长方形OABC的边OC,OA所在直线为x轴、y轴,建立平面直角坐 标系.已知AO=13,AB=5,点E在线段OC上,以直线AE为轴,把△OAE翻折,点O的对应点D恰好落在线段BC上.则点E的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列条件的三角形中,不是直角三角形的是( )
A.∠A-∠B=∠CB.∠A:∠B:∠C=3: 4: 7
C.∠A=2∠B=3∠CD.∠A=9°,∠B=81°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若在一个两位正整数N的个位数字与十位数字之间添上数字6,组成一个新的三位数,我们称这个三位数为N的“至善数”,如34的“至善数为364”;若将一个两位正整数M加6后得到一个新数,我们称这个新数为M的“明德数”,如34的“明德数为40”.
(1)30的“至善数”是 ,“明德数”是 .
(2)求证:对任意一个两位正整数A,其“至善数”与“明德数”之差能被9整除;
(3)若一个两位正整数B的明德数的各位数字之和是B的至善数各位数字之和的一半,求B的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
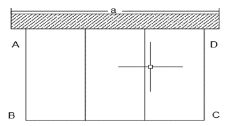
【题目】如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长![]() 米),用木栏围成三个大小相等的长方形,木栏总长24米,总面积为32平方米.
米),用木栏围成三个大小相等的长方形,木栏总长24米,总面积为32平方米.
(1)若墙长![]() 米,求AB、BC的长.
米,求AB、BC的长.
(2)若![]() 米的墙长对鸡舍的长和宽是否有影响?请说明你的理由.
米的墙长对鸡舍的长和宽是否有影响?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD上的点.且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系.

解法探究:小明同学通过思考,得到了如下的解决方法.
延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,从而可得结论.
(1)请先写出小明得出的结论,并在小明的解决方法的提示下,写出所得结论的理由.
解:线段BE、EF、FD之间的数量关系是: .
理由:延长FD到点G,使DG=BE,连结AG.(以下过程请同学们完整解答)
(2)拓展延伸:
如图②,在四边形ABCD中,AB=AD,若∠B+∠D=180°,E、F分别是BC、CD上的点.且∠EAF=![]() ∠BAD,则(1)中的结论是否仍然成立?若成立,请再把结论写一写;若不成立,请直接写出你认为成立的结论.
∠BAD,则(1)中的结论是否仍然成立?若成立,请再把结论写一写;若不成立,请直接写出你认为成立的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com