
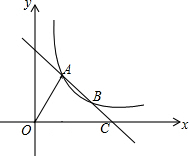
 如图,直线AB交双曲线y=$\frac{k}{x}$于点A,B,交x轴于点C,连结OA,若OA⊥AB,tan∠ACO=$\frac{1}{2}$,S△OAC=12,则k的值为$\frac{24}{5}$.
如图,直线AB交双曲线y=$\frac{k}{x}$于点A,B,交x轴于点C,连结OA,若OA⊥AB,tan∠ACO=$\frac{1}{2}$,S△OAC=12,则k的值为$\frac{24}{5}$. 分析 作AD⊥OC于D,根据已知求得AD=2OD,然后根据勾股定理求得OA=$\sqrt{5}$OD,然后根据三角形相似的性质求得S△DOA=$\frac{12}{5}$,进而根据反比例函数系数k的几何意义即可求得k的值.
解答  解:作AD⊥OC于D,
解:作AD⊥OC于D,
∵∠OAC=∠ADO=90°,∠AOD=∠COA,
∴∠OAD=∠ACO,
∵tan∠ACO=$\frac{1}{2}$,
∴tan∠OAD=$\frac{OD}{AD}$=$\frac{1}{2}$,
∴AD=2OD,
∴OA=$\sqrt{5}$OD,
∴$\frac{OA}{OD}$=$\sqrt{5}$,
∵∠OAC=∠ADO=90°,∠AOD=∠COA,
∴△AOC∽△DOA,
∴$\frac{{S}_{△AOC}}{{S}_{△DOA}}$=($\frac{OA}{OD}$)2=5,
∵S△OAC=12,
∴S△DOA=$\frac{12}{5}$,
∵S△DOA=$\frac{1}{2}$|k|,k>0,
∴k=2×$\frac{12}{5}$=$\frac{24}{5}$,
故答案为$\frac{24}{5}$.
点评 本题考查了反比例函数与一次函数的交点问题,三角形相似的判断和性质以及反比例函数系数k的几何意义,作出辅助线构建相似三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
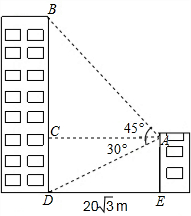 小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20$\sqrt{3}$米.
小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20$\sqrt{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com