
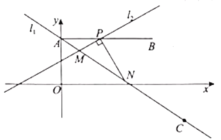
【题目】如图,直线![]() 经过点
经过点![]() 和
和![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是线段
是线段![]() 上的动点(点
上的动点(点![]() 不与点
不与点![]() 重合),直线
重合),直线![]() 经过点
经过点![]() ,并与
,并与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(1)求![]() 的函数表达式;
的函数表达式;
(2)当![]() 时,
时,
①求点![]() 的坐标;
的坐标;
②求![]() .
.
(3)将点![]() 的横坐标记为
的横坐标记为![]() ,在点
,在点![]() 移动的过程中,直接写出
移动的过程中,直接写出![]() 的范围.
的范围.
【答案】(1)![]() 的表达式为
的表达式为![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)
;(3)![]()
【解析】
(1)先设![]() 的方程为y=kx+b,再根据两点确定一条直线,将已知坐标(0,2)、(6,-2)带入方程计算即可;
的方程为y=kx+b,再根据两点确定一条直线,将已知坐标(0,2)、(6,-2)带入方程计算即可;
(2)①将k值带入![]() 方程后,联立方程组即可算出M的坐标;
方程后,联立方程组即可算出M的坐标;
②通过A点与P点纵坐标相同,即可算出P的具体坐标,再根据坐标算出三角形的底和高,应用三角形面积公式即可求出;
(3)由P点的活动范围是AB之间,大致明确![]() 的大小变化,再根据相似三角形算出N点坐标,带入
的大小变化,再根据相似三角形算出N点坐标,带入![]() ,即可算出
,即可算出![]() 的范围.
的范围.
解:(1)设![]() 的表达式为:
的表达式为:![]() ,将点
,将点![]() 和
和![]() 代入,
代入,
求得![]() 的表达式为:
的表达式为:![]() .
.
(2)当![]() 时,
时,
①求得![]() 的表达式为:
的表达式为:![]() ,
,
解方程组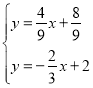 ,求得交点
,求得交点![]() .
.
②当![]() 时,有
时,有![]() ,解得
,解得![]() ,∴
,∴![]() .
.
点![]() 到直线
到直线![]() 的距离是
的距离是![]() .
.
∴![]() .
.
(3)![]()
由题![]() 恒过点
恒过点![]() ,
,![]() 与线段
与线段![]() 有交点,
有交点,
∵点![]() 的运动范围是线段
的运动范围是线段![]() (点
(点![]() 不与点
不与点![]() 重合),
重合),
①点![]() 的横坐标随着
的横坐标随着![]() 变小而变小,即
变小而变小,即![]() 趋于0.
趋于0.
②当![]() 过点
过点![]() 时,此时点
时,此时点![]() 与点
与点![]() 重合,如图所示,
重合,如图所示,
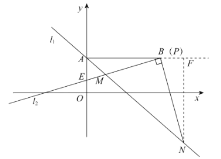
过点![]() 作
作![]() ,
,
∴![]() .∴
.∴![]() .
.
设点![]() ,则
,则![]() ,
,![]() .
.
∵![]() 过点
过点![]() ,其表达式为
,其表达式为![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴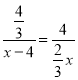 ,
,
∴![]() ,即
,即![]() .
.
∴![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某公司用6000元购进A,B两种电话机25台,购买A种电话机与购买B种电话机的费用相等.已知A种电话机的单价是B种电话机单价的1.5倍.
(1)求A,B两种电话机的单价各是多少?
(2)若计划用不超过8000元的资金再次购进A,B两种话机共30台,已知A,B两种电话机的进价不变,求最多能购进多少台A种电话机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中放入![]() 个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为
个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为![]() 、
、![]() 、
、![]() 克,已知随机的摸出一个鸡蛋,摸到
克,已知随机的摸出一个鸡蛋,摸到![]() 克和
克和![]() 克的鸡蛋的概率是相等的.
克的鸡蛋的概率是相等的.
(1)求这四个鸡蛋质量的众数和中位数
(2)小明做实验需要拿走一个鸡蛋,芳芳在小明拿走后从剩下的三个鸡蛋中随机的拿走一个
①通过计算分析小明拿走一个鸡蛋后,剩下的三个鸡蛋质量的中位数是多少?
②假设小明拿走的鸡蛋质量为![]() 克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是
克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是![]() 克的鸡蛋的概率?
克的鸡蛋的概率?
查看答案和解析>>
科目:初中数学 来源: 题型:
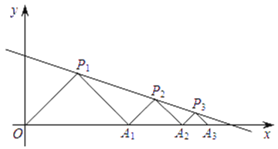
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,...都是等腰直角三角形,其直角顶点
,...都是等腰直角三角形,其直角顶点![]() ,
,![]() ,
,![]() ,...均在直线
,...均在直线![]() 上,设
上,设![]() ,
,![]() ,
,![]() ,...的面积分别为
,...的面积分别为![]() ,
,![]() ,
,![]() ,...,依据图形所反映的规律,S2020=__________.
,...,依据图形所反映的规律,S2020=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,在图中按下列步骤进行尺规作图:
,在图中按下列步骤进行尺规作图:
① | 以 |
② | 分别以 |
③ | 画射线 |
下列说法错误的是( )
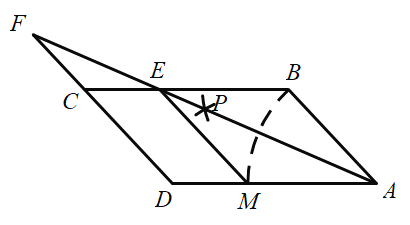
A.![]() B.
B.![]()
C.![]() D.若
D.若![]() ,则
,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
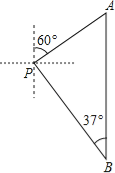
【题目】小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队员在篮球联赛中分别与甲队、乙队对阵各四场,下表是他的技术统计.
场次 | 对阵甲队 | 对阵乙队 | ||
得分(分) | 失误(次) | 得分(分) | 失误(次) | |
第一场 | 25 | 2 | 27 | 3 |
第二场 | 30 | 0 | 31 | 1 |
第三场 | 27 | 3 | 20 | 2 |
第四场 | 26 | 2 | 26 | 4 |
(1)他在对阵甲队和乙队的各四场比赛中,平均每场得分分别是多少?
(2)利用方差判断他在对阵哪个队时得分比较稳定;
(3)根据上表提供的信息,判断他在对阵哪个队时总体发挥较好,简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
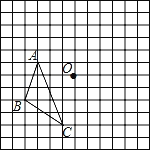
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点![]() ABC(顶点是网格线的交点)和格点O.
ABC(顶点是网格线的交点)和格点O.
(1)平移![]() ABC,使得点A与点O重合,画出平移后的
ABC,使得点A与点O重合,画出平移后的![]() A′B′C′;
A′B′C′;
(2)画出![]() ABC关于点O对称的
ABC关于点O对称的![]() DEF;
DEF;
(3)判断![]() A′B′C′与
A′B′C′与![]() DEF是否成中心对称?
DEF是否成中心对称?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:


(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com