
【题目】△ABC中,最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,如图为其中一种分割法,此时△ABC中的最大内角为90°,那么其它分割法中,△ABC中的最大内角度数为_____.

【答案】117°或108°或84°.
【解析】
根据等腰三角形的性质进行分割,写出△ABC中的最大内角的所有可能值.
①∠BAD=∠BDA=![]() (180°﹣24°)=78°,∠DAC=∠DCA=
(180°﹣24°)=78°,∠DAC=∠DCA=![]() ∠BDA=39°,如图1所示:
∠BDA=39°,如图1所示:

∴∠BAC=78°+39°=117°;
②∠DBA=∠DAB=24°,∠ADC=∠ACD=2∠DBA=48°,如图2所示:

∴∠DAC=180°﹣2×48°=84°,
∴∠BAC=24°+84°=108°;
③∠DBA=∠DAB=24°,∠ADC=∠DAC=2∠DBA=48°,如图3所示:

∴∠BAC=24°+48°=72°,∠C=180°﹣2×48°=84°;
∴其它分割法中,△ABC中的最大内角度数为117°或108°或84°,
故答案为:117°或108°或84°.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:
【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求这块四边形空地的面积;
(2)若每平方米草皮需要200元,问学校需要投入多少资金买草皮?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D、E分别是BC、AC上的动点且BD=CE,连接AD与BE相交于点F,连接CF,下列结论:①△ABD≌△BCE;②∠AFB=120°;③若BD=CD,则FA=FB=FC;④∠AFC=90°,则AF=3BF,其中正确的结论共有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,且
,且![]() 面积是24,
面积是24,![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 边于点
边于点![]() ,若点
,若点![]() 为
为![]() 边的中点,点
边的中点,点![]() 为线段
为线段![]() 上一动点,则
上一动点,则![]() 周长的最小值为( )
周长的最小值为( )

A.9B.10C.11D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,求证:
,求证:![]() .
.

(2)如图2,四边形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,连接
上,连接![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.
①找出图中与![]() 相等的线段,并加以证明;
相等的线段,并加以证明;
②求![]() 的度数(用含
的度数(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
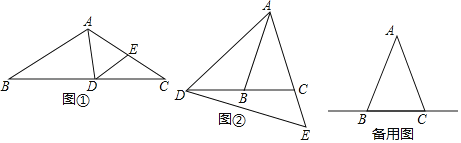
【题目】如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.
⑴如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;
⑵如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;
⑶当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形(长方形)![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,点
重合,点![]() 落在
落在![]() 处,连接
处,连接![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,
,![]() ,
,![]() 三点在同一直线上,其中正确的是( )
三点在同一直线上,其中正确的是( )

A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜀山区植物园是一座三面环水的半岛园区,拥有梅园、桂花园、竹园、木兰园、水景园等示范区。为了种植植物,需要从甲乙两地向园区A,B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A,B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需费用)。
运费(元/吨) | ||
A | B | |
甲地 | 12 | 12 |
乙地 | 10 | 8 |
运往A、B两地的吨数 | ||
A | B | |
甲地 | x | 50-x |
乙地 | ( ) | ( ) |
(1)设甲地运往A棚营养土x吨,请用关于x的代数式完成上表;
(2)设甲地运往A棚营养土x吨,求总运费y(元)关于x(吨)的函数关系式(要求写出变量取值范围);
(3)当甲、乙两地各运往A、B两棚多少吨营养土时,总运费最省?最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 内接于
内接于![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 的切线与
的切线与![]() 的延长线交于点
的延长线交于点![]() .
.

![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长;
的长;
![]() 在题设条件下,为使
在题设条件下,为使![]() 是平行四边形,
是平行四边形,![]() 应满足怎样的条件(不要求证明).
应满足怎样的条件(不要求证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com