
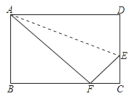
【题目】如图已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为___________.
【答案】3cm
【解析】
要求CE的长,应先设CE的长为x,由将△ADE折叠使点D恰好落在BC边上的点F可得Rt△ADE≌Rt△AFE,所以AF=10cm,EF=DE=8-x;在Rt△ABF中由勾股定理得:AB2+BF2=AF2,已知AB、AF的长可求出BF的长,又CF=BC-BF=10-BF,在Rt△ECF中由勾股定理可得:EF2=CE2+CF2,即:(8-x)2=x2+(10-BF)2,将求出的BF的值代入该方程求出x的值,即求出了CE的长.
∵四边形ABCD是矩形,
∴AD=BC=10cm,CD=AB=8cm,
根据题意得:Rt△ADE≌Rt△AFE,
∴∠AFE=90°,AF=10cm,EF=DE,
设CE=xcm,则DE=EF=CDCE=(8x)cm,
在Rt△ABF中由勾股定理得:AB2+BF2=AF2,
即82+BF2=102,
∴BF=6cm,
∴CF=BCBF=106=4(cm),
在Rt△ECF中,由勾股定理可得:EF2=CE2+CF2,
即(8x)2=x2+42,
∴6416x+x2=x2+16,
∴x=3(cm),
即CE=3cm.
故答案为:3cm.


科目:初中数学 来源: 题型:
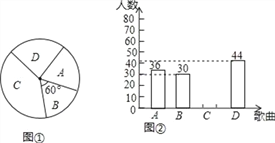
【题目】为庆祝建军90周年,某校计划在五月份举行“唱响军歌”歌咏比赛,要确定一首喜欢人数最多的歌曲为每班必唱歌曲.为此提供代号为A,B,C,D四首备选曲目让学生选择,经过抽样调查,并将采集的数据绘制如下两幅不完整的统计图.请根据图①,图②所提供的信息,
解答下列问题:
(1)本次抽样调查中,选择曲目代号为A的学生占抽样总数的百分比为 ;
(2)请将图②补充完整;
(3)若该校共有1260名学生,根据抽样调查的结果估计全校共有多少学生选择喜欢人数最多的歌曲?(要有解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
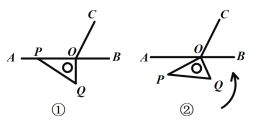
【题目】如图①,![]() 为直线
为直线![]() 上一点,作射线
上一点,作射线![]() ,使
,使![]() ,将一个直角三角尺如图摆放,直角顶点在点
,将一个直角三角尺如图摆放,直角顶点在点![]() 处,一条直角边
处,一条直角边![]() 在射线
在射线![]() 上. 将图
上. 将图![]() 中的三角尺绕点
中的三角尺绕点![]() 以每秒10°的速度按逆时针方向旋转(如图②所示),在旋转一周的过程中,第
以每秒10°的速度按逆时针方向旋转(如图②所示),在旋转一周的过程中,第![]() 秒时,
秒时,![]() 所在直线恰好平分
所在直线恰好平分![]() ,则
,则![]() 的值为_________.
的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如下:
自选项目 | 人数 | 频率 |
立定跳远 | 9 | 0.18 |
三级蛙跳 | 12 | a |
一分钟跳绳 | 8 | 0.16 |
投掷实心球 | b | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
(1)求a,b的值;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至多有一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
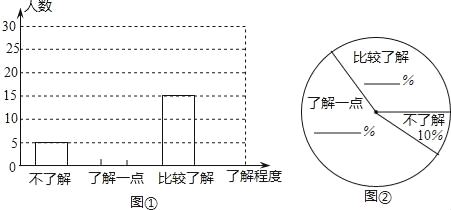
【题目】某校八年级共有800名学生,准备调查他们对“低碳”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案:
方案一:调查八年级部分女生;
方案二:调查八年级部分男生;
方案三:到八年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是_____;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将两个统计图补充完整;
(3)请你估计该校八年级约有多少名学生比较了解“低碳”知识.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】特殊两位数乘法的速算——如果两个两位数的十位数字相同,个位数字相加为10,那么能立说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C,B+C=10,A>3),那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.
如:47×43=2021,61×69=4209.
(1)请你直接写出83×87的值;
(2)设这两个两位数的十位数字为x(x>3),个位数字分别为y和z(y+z=10),通过计算验证这两个两位数的乘积为100x(x+1)+yz.
(3)99991×99999=___________________(直接填结果)
【答案】7221
【解析】分析:![]() 套用上面的归纳总结代入数据,即可得出结论;
套用上面的归纳总结代入数据,即可得出结论;
![]() 利用上面总结的结论套入数据表示出该两个两位数的成绩,在将等式展开合并同类项得出左边=右边,从而证明结论成立.
利用上面总结的结论套入数据表示出该两个两位数的成绩,在将等式展开合并同类项得出左边=右边,从而证明结论成立.
![]() 直接运算即可.
直接运算即可.
详解:(1)83和87满足题中的条件,即十位数都是8,8>3,且个位数字分别是3和7,之和为10,那么它们的乘积是一个4位数,前两位数字是8和9的乘积,后两位数字就是3和7的乘积,因而,答案为:7221.
(2) 这两个两位数的十位数字为x(x>3),个位数字分别为y和z,则由题知y+z=10,
因而有:(10x+y)(10x+z)=100x2+10xz+10xy+yz
=100x2+10x(y+z)+yz,
=100x2+100x+yz,
=100x(x+1)+yz.
(3)9999000009.
点睛:通过阅读题干掌握题中所给信息得出推理方法,然后通过多项式的展开式得出答案.学生应熟练掌握归纳推理的数学思想.
【题型】解答题
【结束】
19
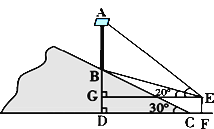
【题目】为了大力弘扬和践行社会主义核心价值观,某乡镇在一条公路旁的小山坡上,树立一块大型标语牌AB,如图所示,标语牌底部B点到山脚C点的距离BC为20米,山坡的坡角为30°. 某同学在山脚的平地F处测量该标语牌的高,测得点C到测角仪EF的水平距离CF = 1.7米,同时测得标语牌顶部A点的仰角为45°,底部B点的仰角为20°,求标语牌AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com