练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．某轮船顺水航行3h，逆水航行1.5h，已知轮船在静水中的速度是akm/h，水流的速度为bkm/h，轮船共航行多少千米？

    分析 根据静水速度+水流速度=顺水速度，静水速度-水流速度=逆水速度，分别表示出顺水与逆水速度，根据题意列出关系式，去括号合并即可得到结果．

    解答 解：根据题意得：3（a+b）+1.5（a-b）=4.5a+1.5b，
    则轮船共航行（4.5a+1.5b）千米

    点评 此题考查列代数式，整式的加减，涉及的知识有：去括号法则，以及合并同类项法则，熟练掌握法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

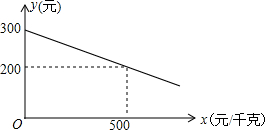    14．某企业生产一种环保产品，需要添加一种稀少材料的新型原料，若每件产品的利润与新型原料价格成一次函数关系，且每件产品的利润y（元）与新型原料的价格x（元/千克）的函数图象如图：
    （1）当新型原料的价格为400元/千克时，每件产品的利润是多少？
    （2）为了珍惜资源，政府部门规定：每天使用量m（千克）与价格x（元/千克）的函数关系为m=$\frac{1}{10}$x-50，且1千克新型原料可生产10件产品．那么生产200件这种产品，一共可得利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．当a≥0时，|a|=a；当a≤0时，|a|=-a．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，已知A，B，C是半径为1的⊙O上三点，且四边形AOBC是平行四边形，则弦AB的长是$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知关于x的方程kx2+（2k+1）x+2=0．
    （1）若方程有两个不相等的实数根，则k的取值范围是k≠$\frac{1}{2}$且k≠0；
    （2）求证：无论k取任何实数时，方程总有实数根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列命题中，假命题是（　　）
    A．四个内角都相等的四边形是矩形
    B．四条边都相等的平行四边形是正方形
    C．既是菱形又是矩形的四边形是正方形
    D．对角线互相垂直的平行四边形是菱形

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．若抛物线y=x2+3x+a与x轴只有一个交点，求实数a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

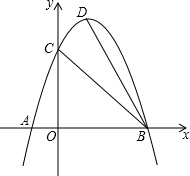    13．如图，抛物线y=-x2+2x+3与x轴交于A、B两点，交y轴正半轴于C点，D为抛物线的顶点，点P在x轴上，且∠PCB=∠CBD，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

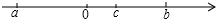    14．（1）有理数a，b，c在数轴上的位置如图所示，且|a|=|b|，化简
    |a-c|+|b-c|+|a+b|．
    （2）-2a2by+1与7b3a2是同类项，求代数式：3x2-6y2+3（xy-3y2）-（3x2+3xy+7y2）的值．

    查看答案和解析>>

    同步练习册答案