
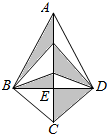
 在四边形ABCD中,AC⊥BD于E,且BE=DE,已知AC=10,BD=5,则图中阴影部分的面积=12.5.
在四边形ABCD中,AC⊥BD于E,且BE=DE,已知AC=10,BD=5,则图中阴影部分的面积=12.5. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,直线AC:y=$\frac{4}{3}$x+8分别交X轴、y轴于A、C,将△AOC沿y轴翻折得△DOC,并将△AOC绕AC边中点旋转180°得△CBA,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且保证∠CEF的正切值一直为$\frac{4}{3}$.
在平面直角坐标系中,直线AC:y=$\frac{4}{3}$x+8分别交X轴、y轴于A、C,将△AOC沿y轴翻折得△DOC,并将△AOC绕AC边中点旋转180°得△CBA,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且保证∠CEF的正切值一直为$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
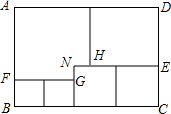 如图,用三种大小不同的五个正方形和一个缺角的长方形拼成长方形ABCD,其中,NH=NG=1cm,设BF=acm.
如图,用三种大小不同的五个正方形和一个缺角的长方形拼成长方形ABCD,其中,NH=NG=1cm,设BF=acm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
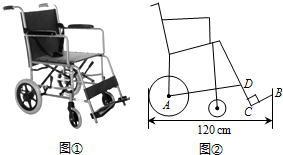 为了应对人口老龄化问题,国家大力发展养老事业.某养老机构定制轮椅供行动不便的老人使用.图①是一种型号的手动轮椅实物图,图②为其侧面示意图,该轮椅前后长度为120cm,后轮半径为24cm,CB=CD=24cm,踏板CB与CD垂直,横档AD、踏板CB与地面所成的角分别为15°、30°.求:
为了应对人口老龄化问题,国家大力发展养老事业.某养老机构定制轮椅供行动不便的老人使用.图①是一种型号的手动轮椅实物图,图②为其侧面示意图,该轮椅前后长度为120cm,后轮半径为24cm,CB=CD=24cm,踏板CB与CD垂直,横档AD、踏板CB与地面所成的角分别为15°、30°.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com