
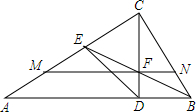
 如图,在△ABC中,∠C=90°,CD⊥AB于D,BE为∠ABC的角平分线,BE交CD于点F,M为线段AC上一点,且AM=EC,直线MF与CB交于点N.求证:DE⊥DN.
如图,在△ABC中,∠C=90°,CD⊥AB于D,BE为∠ABC的角平分线,BE交CD于点F,M为线段AC上一点,且AM=EC,直线MF与CB交于点N.求证:DE⊥DN. 分析 过E作EG⊥AB于G,连接BF,根据角平分线的性质得到CE=GE,证得Rt△BGE≌Rt△BCE,得到BC=BG,通过△BGF≌△BCF,得到CF=GF,根据余角和外角的性质得到∠CEF=∠CFE,推出CE=CF,求出四边形CEGF是菱形,由菱形的性质得到GF∥AC,求出四边形AGFM是平行四边形,根据平行四边形的性质得到MN∥AB,由于△CMN∽△CAB,得到$\frac{CM}{CA}=\frac{CN}{BC}$,$\frac{CM}{CN}=\frac{CA}{BC}$,等量代换得到$\frac{AE}{CN}=\frac{AD}{CD}$,证得△ADE∽△CND,根据相似三角形的性质得到∠EDA=∠CDN,由∠CDA=∠CDE+∠EDA=90°,于是得到结论.
解答 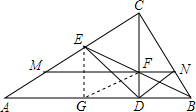 解:过E作EG⊥AB于G,连接BF,
解:过E作EG⊥AB于G,连接BF,
∵BE为∠ABC的角平分线,∠C=90°,
∴CE=GE,
在Rt△BGE与Rt△BCE中,$\left\{\begin{array}{l}{CE=GE}\\{BE=BE}\end{array}\right.$,
∴Rt△BGE≌Rt△BCE,
∴BC=BG,
在△BGF与△BCF中,$\left\{\begin{array}{l}{BC=BG}\\{∠CBF=∠GBF}\\{BF=BF}\end{array}\right.$,
∴△BGF≌△BCF,
∴CF=GF,
∵CD⊥AB,
∴∠A+∠B=∠BCD+∠B=90°,
∴∠A=∠DCB,
∵∠CEB=∠EBA+∠A,∠CFE=∠FBC+∠FCB,
∴∠CEF=∠CFE,
∴CE=CF,
∴CE=CF=GF=GE,
∴四边形CEGF是菱形,
∴GF∥AC,
∵AM=CE,
∴AM=FG,
∴四边形AGFM是平行四边形,
∴MN∥AB,
∴CD⊥MN,
∴∠CMN=∠A,
∴△CMN∽△CAB,
∴$\frac{CM}{CA}=\frac{CN}{BC}$,$\frac{CM}{CN}=\frac{CA}{BC}$,
∵$\frac{CA}{BC}=\frac{AD}{CD}$,
∴$\frac{AE}{CN}=\frac{AD}{CD}$,
∵∠A=∠DCN,
∴△ADE∽△CND,
∴∠EDA=∠CDN,
∵∠CDA=∠CDE+∠EDA=90°,
∴∠EDN=∠CDE+∠CDN=∠CDE+∠EDA=90°,
∴DE⊥DN.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,菱形的判定和性质,垂直的定义,正确的作出辅助线是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 现有一块边长为a的正方形草坪,如图所示,将其相邻两边均扩大b,用两种方法计算扩大后草坪的面积.由此验证我们所学过的一个非常熟悉的公式,并写出这个公式.
现有一块边长为a的正方形草坪,如图所示,将其相邻两边均扩大b,用两种方法计算扩大后草坪的面积.由此验证我们所学过的一个非常熟悉的公式,并写出这个公式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 △ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )
△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )| A. | 2.5 | B. | 3 | C. | 2.25或3 | D. | 1或5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把Rt△ABC的斜边放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置,设BC=1,AC=$\sqrt{3}$,求当顶点A运动到A″位置时,点A经过的路径长度.
如图,把Rt△ABC的斜边放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置,设BC=1,AC=$\sqrt{3}$,求当顶点A运动到A″位置时,点A经过的路径长度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com