
【题目】已知正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,当∠MAN绕点A旋转到BM=DN时(如图1),则
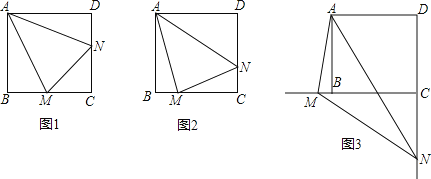
(1)线段BM、DN和MN之间的数量关系是______;
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
(3)当∠MAN绕点A旋转到(如图3)的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
【答案】(1)BM+DN=MN;(2)BM+DN=MN,证明详见解析;(3)DN-BM=MN,证明详见解析.
【解析】
(1)连接AC,交MN于点G,则可知AC垂直平分MN,结合∠MAN=45°,可证明△ABM≌△AGM,可得到BM=MG,同理可得到NG=DN,可得出结论;
(2)在MB的延长线上,截取BE=DN,连接AE,则可证明△ABE≌△ADN,可得到AE=AN,进一步可证明△AEM≌△ANM,可得结论BM+DN=MN;
(3)在DC上截取DF=BM,连接AF,可先证明△ABM≌△ADF,进一步可证明△MAN≌△FAN,可得到MN=NF,从而可得到DN﹣BM=MN.
(1)如图1,连接AC,交MN于点G.
∵四边形ABCD为正方形,∴BC=CD,且BM=DN,∴CM=CN,且AC平分∠BCD,∴AC⊥MN,且MG=GN,∴AM=AN.
∵AG⊥MN,∴∠MAG=∠NAG.
∵∠BAC=∠MAN=45°,即∠BAM+∠GAM=∠GAM+∠GAN,∴∠BAM=∠GAN=∠GAM.
在△ABM和△AGM中,∵ ,∴△ABM≌△AGM(AAS),∴BM=MG,同理可得GN=DN,∴BM+DN=MG+GN=MN.
,∴△ABM≌△AGM(AAS),∴BM=MG,同理可得GN=DN,∴BM+DN=MG+GN=MN.
故答案为:BM+DN=MN;
(2)猜想:BM+DN=MN,证明如下:
如图2,在MB的延长线上,截取BE=DN,连接AE.
在△ABE和△ADN中,∵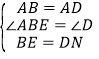 ,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD.
,∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD.
∵∠BAD=90°,∠MAN=45°,∴∠BAM+∠DAN=45°,∴∠EAB+∠BAM=45°,∴∠EAM=∠NAM.
在△AEM和△ANM中,∵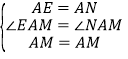 ,∴△AEM≌△ANM(SAS),∴ME=MN,又ME=BE+BM=BM+DN,∴BM+DN=MN;
,∴△AEM≌△ANM(SAS),∴ME=MN,又ME=BE+BM=BM+DN,∴BM+DN=MN;
(3)DN﹣BM=MN.证明如下:
如图3,在DC上截取DF=BM,连接AF.
△ABM和△ADF中,∵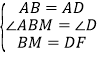 ,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即∠MAF=∠BAD=90°.
,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即∠MAF=∠BAD=90°.
∵∠MAN=45°,∴∠MAN=∠FAN=45°.
在△MAN和△FAN中,∵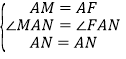 ,∴△MAN≌△FAN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN.
,∴△MAN≌△FAN(SAS),∴MN=NF,∴MN=DN﹣DF=DN﹣BM,∴DN﹣BM=MN.


科目:初中数学 来源: 题型:
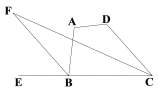
【题目】如图,四边形ABCD的内角∠DCB与外角∠ABE的平分线相交于点F.
(1)若BF∥CD,∠ABC=80°,求∠DCB的度数;
(2)已知四边形ABCD中,∠A=105,∠D=125,求∠F的度数;
(3)猜想∠F、∠A、∠D之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明袋子中有![]() 个红球,
个红球,![]() 个绿球和
个绿球和![]() 个白球,这些球除颜色外无其他差别.
个白球,这些球除颜色外无其他差别.
![]() 从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该实验,发现摸到绿球的频率稳定于
从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该实验,发现摸到绿球的频率稳定于![]() ,求
,求![]() 的值;
的值;
![]() 在一个摸球游戏中,若有
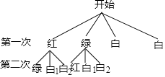
在一个摸球游戏中,若有![]() 个白球,小明用画树状图的方法寻求他两次摸球(摸出一球后,不放回,再摸出一球)的所有可能结果,如图是小明所画的正确树状图的一部分,补全小明所画的树状图,并求两次摸出的球颜色不同的概率.
个白球,小明用画树状图的方法寻求他两次摸球(摸出一球后,不放回,再摸出一球)的所有可能结果,如图是小明所画的正确树状图的一部分,补全小明所画的树状图,并求两次摸出的球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(![]() ,y2)是抛物线上两点,则
,y2)是抛物线上两点,则
y1>y2.其中说法正确的是( )
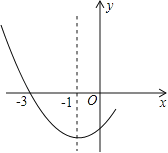
A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法:①△ABD 和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的是( )
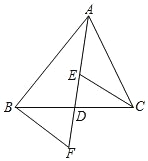
A. ①② B. ③⑤ C. ①③④ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中正确的结论有( )
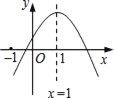
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C、A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
(1)求经过O、A、B三点的抛物线解析式;
(2)求S与t的函数关系式;
(3)将△OPQ绕着点P顺时针旋转90°,是否存在t,使得△OPQ的顶点O或Q在抛物线上?若存在,直接写出t的值;若不存在,请说明理由.
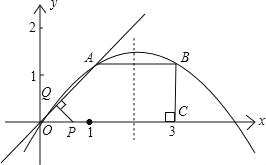
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;
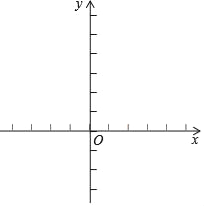
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com