考点:角平分线的性质
专题:证明题
分析:(1)根据角平分线上的点到角的两边距离相等可得点D到AB、AC的距离相等,再根据等高的三角形的面积的比等于底边的比解答;
(2)过点C作CE∥AB与AD的延长线相交于点E,根据两直线平行,内错角相等可得∠BAD=∠E,然后求出△ABD和△ECD相似,根据相似三角形对应边成比例可得
=
,根据角平分线的定义可得∠BAD=∠CAD,再求出∠CAD=∠E,根据等角对等边可得AC=CE,从而得证.
解答:证明:(1)∵AD平分∠BAC,
∴点D到AB、AC的距离相等,设为h,
则S
△ABD=
AB•h,S
△ACD=
AC•h,
∴S
△ABD:S
△ACD=AB:AC;
(2)如图,过点C作CE∥AB与AD的延长线相交于点E,
所以,∠BAD=∠E,
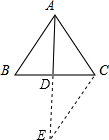
∵∠ADB=∠EDC,
∴△ABD∽△ECD,
∴
=
,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠CAD=∠E,
∴AC=CE,
∴
=
,
即BD:CD=AB:AC.
点评:本题考查了角平分线,相似三角形的判定与性质,主要利用了角平分线上的点到角的两边距离相等的性质,等高的三角形的面积的比等于底边的比的证明,难点在于(2)作辅助线构造出相似三角形和等腰三角形.

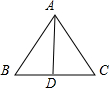 如图,在△ABC中,AD平分∠BAC.求证:
如图,在△ABC中,AD平分∠BAC.求证:

