
【题目】△ABC中,BC=12, 高AD=8,矩形EFGH的一边GH在BC上,顶点E、F分别在AB、AC上,AD与EF交于点M.
(1)求证:![]() ;
;
(2)矩形EFGH可以为正方形吗?若能,请求出正方形的面积,若不能,请说明理由;
(3)设EF=x, EH=y,设矩形EFGH的面积为S,求S与x之间的函数表达式,并求出S的最值.
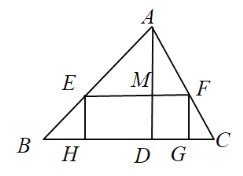
【答案】(1)见解析;(2)能,SEHGF=![]() ;(3)S=-
;(3)S=-![]() x2+8x,当x=6时S最大=24
x2+8x,当x=6时S最大=24
【解析】
(1)先判断出AM是△AEF的高,再判断出△AEF∽△ABC,即可得出结论;
(2)假设EFGH为正方形设EF=m,则AM=8-m,列出方程![]() 求出m的值即可得出答案;
求出m的值即可得出答案;
(3)先判断出四边形EMDG是矩形,得出DM=EH,进而表示出AM=8﹣y,借助(1)的结论即可得出结论;由矩形的面积公式得出函数关系式,即可得出结论.
(1)证明:∵矩形EFGH
∴EF∥BC
∵AD⊥BC
∴AD⊥EF
又∵△AEF∽△ABC
∴![]()
(2)能,解:假设EFGH为正方形设EF=m
∴AM=8-m
∴![]()
∴m=![]()
∴假设成立SEHGF=![]()
(3)∵EH=y
∴AM=8-y
∵![]()
∴![]()
∴y=8-![]() x
x
∵S=xy
∴S=x(8-![]() x)
x)
∴S=-![]() x2+8x=-
x2+8x=-![]() (x-6)2+24
(x-6)2+24
∴a=-![]() <0、
<0、
∴当x=6时S最大=24


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将一枚跳棋放在七边形ABCDEFG的顶点A处,按顺时针方向移动这枚跳棋2020次.移动规则是:第k次移动k个顶点(如第一次移动1个顶点,跳棋停留在B处,第二次移动2个顶点,跳棋停留在D处),按这样的规则,在这2020次移动中,跳棋不可能停留的顶点是( )

A.C、EB.E、FC.G、C、ED.E、C、F
查看答案和解析>>
科目:初中数学 来源: 题型:
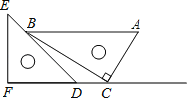
【题目】三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有三张卡片,分别标有数字1,2,3,这些卡片除数字不同外其余均相同.小明从盒子中随机抽取一张卡片记下数字后放回,洗匀后再随机抽取一张卡片.用画树状图或列表的方法,求第二次抽取卡片上的数字小于第一次抽取卡片上的数字的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知∠A=90°, BD=4,CF=6, 则AO的长是 ( )

A.![]() B.
B.![]() C.
C.![]() D.4
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 的函数图象经过
的函数图象经过![]() 两点,过
两点,过![]() 两点作一直线.
两点作一直线.
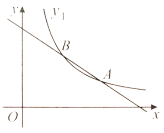
(1)求反比例函数解析式;
(2)将反比例函数![]() 向下平移1个单位,得函数
向下平移1个单位,得函数![]() ________;函数
________;函数![]() 与坐标轴的交点为__________;
与坐标轴的交点为__________;
(3)将直线![]() 向下平移
向下平移![]() 个单位后与函数
个单位后与函数![]() 的图象有唯一交点,求
的图象有唯一交点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=![]() +
+![]() =1.
=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°-α)=1.
(1)当α=30°时,验证sin2α+sin2(90°-α)=1是否成立;
(2)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( )
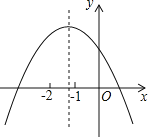
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
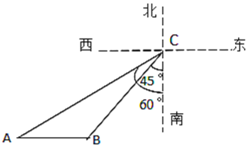
【题目】如图所示,在某海域,一艘指挥船在![]() 处收到渔船在
处收到渔船在![]() 处发出的求救信号,经确定,遇险抛锚的渔船所在的
处发出的求救信号,经确定,遇险抛锚的渔船所在的![]() 处位于
处位于![]() 处的南偏西45°方向上,且
处的南偏西45°方向上,且![]() 海里;指挥船搜索发现,在
海里;指挥船搜索发现,在![]() 处的南偏西60°方向上有一艘海监船
处的南偏西60°方向上有一艘海监船![]() ,恰好位于
,恰好位于![]() 处的正西方向.于是命令海监船
处的正西方向.于是命令海监船![]() 前往搜救,已知海监船
前往搜救,已知海监船![]() 的航行速度为30海里/小时,问渔船在
的航行速度为30海里/小时,问渔船在![]() 处需要等待多长时间才能得到海监船
处需要等待多长时间才能得到海监船![]() 的救援?(参考数据:
的救援?(参考数据:![]() 、
、![]() 、
、![]() 结果精确到0.1小时)
结果精确到0.1小时)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com