
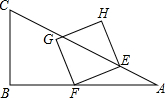
 如图,在△ABC中,∠B=90°,AB=4,BC=2,点E从点A出发,以每秒$\sqrt{5}$个单位长度的速度沿边AC向终点C运动,E点出发的同时,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F逆时针旋转90°得到线段FG,以EF、FG为边作正方形EFGH,设点F运动的时间为t秒(t>0)
如图,在△ABC中,∠B=90°,AB=4,BC=2,点E从点A出发,以每秒$\sqrt{5}$个单位长度的速度沿边AC向终点C运动,E点出发的同时,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F逆时针旋转90°得到线段FG,以EF、FG为边作正方形EFGH,设点F运动的时间为t秒(t>0)分析 (1)作垂线段ED,根据三角函数求DE的长,即是点E到边AB的距离;
(2)当点G落在边AB上时,如图2,此时EF⊥AB,根据同角的三角函数列式可求得t的值;
(3)分两种情况:①当0≤t≤1时,如图3,作高线GP,根据△GPF≌△FDE,则GP=DF=4-4t,代入面积公式求S即可;②当1<t≤2时,如图4,同理作高线求出结论;
(4)当E与C重合,F与A重合时,AH=CG,则t=2.
解答 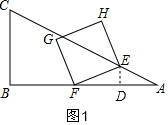 解:(1)如图1,过E作ED⊥AB于D,
解:(1)如图1,过E作ED⊥AB于D,
由题意得:AE=$\sqrt{5}t$,
Rt△ABC中,由勾股定理得:AC=$\sqrt{B{C}^{2}+A{B}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
sin∠A=$\frac{DE}{AE}$=$\frac{BC}{AC}$,
∴$\frac{DE}{\sqrt{5}t}$=$\frac{2}{2\sqrt{5}}$,
∴DE=t,
则点E到边AB的距离是t;
(2)当点G落在边AB上时,如图2,此时EF⊥AB,
由(1)得:EF=t,
∵BF=2t,
∴AF=4-2t,
tan∠A=$\frac{BC}{AB}$=$\frac{EF}{AF}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴$\frac{t}{4-2t}$=$\frac{1}{2}$,
t=1;
(3)分两种情况:
①当0≤t≤1时,如图3,过E作ED⊥AB于D,过G作GP⊥AB于P,
∵ED=t,AD=2t,BF=2t,
∴FD=4-4t,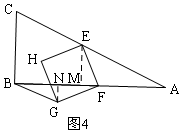
易证△GPF≌△FDE,
∴GP=DF=4-4t,
∴S=S△BFG=$\frac{1}{2}$BF•GP=$\frac{1}{2}×2t$×(4-4t)=-4t2+4t(0≤t≤1);
②当1<t≤2时,如图4,过E作EM⊥BC于M,过G作GN⊥BC于N,
易证△EMF≌△FNG,
∴GN=FM,
∴EM=t,AM=2t,
∴BM=4-2t,
∴FM=GN=2t-(4-2t)=4t-4,
∴S=S△BFG=$\frac{1}{2}$BF•GN=$\frac{1}{2}×2t$×(4t-4)=4t2-4t(1<t≤2);
综上所述,S与t之间的函数关系式为:
S=$\left\{\begin{array}{l}{-4{t}^{2}+4t(0≤t≤1)}\\{4{t}^{2}-4t(1<t≤2)}\end{array}\right.$;
(4)正方形EFGH的顶点H,G分别与点A,C距离相等时,如图5,此时E与C重合,F与A重合,
∴t=2.
点评 本题是四边形的综合题,考查了正方形的性质、全等三角形的判定和性质、勾股定理的运用以及三角形面积的求法等知识点.试题难度不大,需要注意的是(3)问中,在两动点运动过程中,△BFG的面积符合一个函数关系式,本题的关键是用含时间的代数式准确表示BF和AE的长度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | a $\sqrt{12ab}$ | B. | 12a2b | C. | a2$\sqrt{12b}$ | D. | 2a $\sqrt{3b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,甲、乙两盏路灯相距20米,一天晚上,当小刚从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小刚的身高为1.6米,那么路灯甲的高为8米.
如图,甲、乙两盏路灯相距20米,一天晚上,当小刚从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小刚的身高为1.6米,那么路灯甲的高为8米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 62500 | B. | 1000 | C. | 500 | D. | 250 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程.
有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com