
 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:| t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | … |
| x(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
| y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |

分析 (1)①根据描出了上表中y与t各对对应值为坐标的点,画出该函数的图象即可;
②利用网格中数据直接得出乒乓球达到最大高度时的时间;
(2)首先求出函数解析式,进而求出乒乓球落在桌面时,与端点A的水平距离.
解答 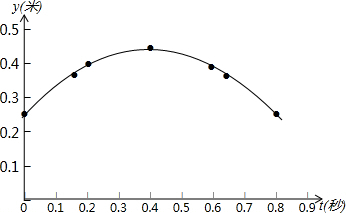 解:(1)①如图所示,
解:(1)①如图所示,
②由表格中数据可得,t=0.4(秒),乒乓球达到最大高度;
(2)由表格中数据,可设y=a(x-1)2+0.45,
将(0,0.25)代入,可得:a=-$\frac{1}{5}$,
则y=-$\frac{1}{5}$(x-1)2+0.45,
当y=0时,0=-$\frac{1}{5}$(x-1)2+0.45,
解得:x1=$\frac{5}{2}$,x2=-$\frac{1}{2}$(舍去),
即乒乓球与端点A的水平距离是$\frac{5}{2}$m.
点评 此题主要考查了二次函数对应用以及根的判别式和一元二次方程的解法等知识,利用图表中数据得出函数解析式是解题关键.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线$y=\frac{1}{2}{x^2}+bx+c$经过点A(0,2)和B(1,$\frac{3}{2}$).
在平面直角坐标系xOy中,抛物线$y=\frac{1}{2}{x^2}+bx+c$经过点A(0,2)和B(1,$\frac{3}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象经过点(2,-1) | B. | 图象位于第二、四象限 | ||
| C. | 当x<0时,y随x的增大而减小 | D. | 当x>0时,y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com