练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

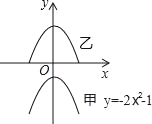
    【题目】已知抛物线甲：y=﹣2x2﹣1和抛物线乙的形状相同，且两条抛物线的对称轴均为y轴，两点距离5个单位长度，它们的图象如图所示，则抛物线乙的解析式为______．

    【答案】y=﹣2x2+4．

    【解析】

    设抛物线乙的解析式为y=ax2+bx+c，先抛物线甲：y=﹣2x2﹣1和抛物线乙的形状相同，且两条抛物线的对称轴均为y轴，得出a=﹣2，b=0，再由两点距离5个单位长度，结合图形得出c﹣（﹣1）=5，求出c=4．从而确定抛物线乙的解析式．

    设抛物线乙的解析式为y=ax2+bx+c．

    ∵抛物线甲：y=﹣2x2﹣1和抛物线乙的形状相同，且两条抛物线的对称轴均为y轴，∴a=﹣2，b=0．

    又∵两点距离5个单位长度，∴c﹣（﹣1）=5，∴c=4．

    即y=﹣2x2+4．

    故答案为：y=﹣2x2+4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为厉行节能减排，倡导绿色出行，今年3月以来．“共享单车”（俗称“小黄车”）公益活动登陆我市中心城区，某公司拟在甲、乙两个街道社区投放一批“小黄车”，这批自行车包括A、B两种不同款型，请回答下列问题：

    问题1：单价

    该公司早期在甲街区进行了试点投放，共投放A、B两型自行车各50辆，投放成本共计7500元，其中B型车的成本单价比A型车高10元，A、B两型自行车的单价各是多少？

    问题2：投放方式

    该公司决定采取如下投放方式：甲街区每1000人投放a辆“小黄车”，乙街区每1000人投放 辆“小黄车”，按照这种投放方式，甲街区共投放1500辆，乙街区共投放1200辆，如果两个街区共有15万人，试求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

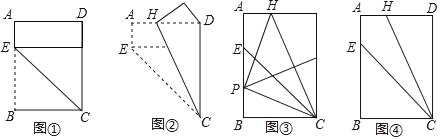
    【题目】对给定的一张矩形纸片ABCD进行如下操作：先沿CE折叠，使点B落在CD边上（如图①），再沿CH折叠，这时发现点E恰好与点D重合（如图②）

    （1）根据以上操作和发现，求的值；

    （2）将该矩形纸片展开．

    ①如图③，折叠该矩形纸片，使点C与点H重合，折痕与AB相交于点P，再将该矩形纸片展开．求证：∠HPC=90°；

    ②不借助工具，利用图④探索一种新的折叠方法，找出与图③中位置相同的P点，要求只有一条折痕，且点P在折痕上，请简要说明折叠方法．（不需说明理由）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一列快车由甲地开往乙地，一列慢车由乙地开往甲地，两车同时出发，匀速运动，快车离乙地的路程（）与行驶的时间（）之间的函数关系，如图中线段所示，慢车离乙地的路程（）与行驶的时间（）之间的函数关系，如图中线段所示，则快、慢车相距225时，行驶的时间是（ ）

    A.1B.3C.1或3D.2或4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形中，，，于，

    （1）求证：；

    （2）若，，求四边形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将半径为2，圆心角为120°的扇形OAB绕点A逆时针旋转60°，点O，B的对应点分别为O′，B′，连接BB′，则图中阴影部分的面积是( )

    A. B. 2－ C. 2－ D. 4－

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小红用一张长方形纸片ABCD进行折纸，已知该纸片宽AB为8cm，长BC为10cm．当小红折叠时，顶点D落在BC边上的点F处（折痕为AE）．想一想，此时EC有多长？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，，的平分线与BC的延长线交于点E，与DC交于点F，且点F为边DC的中点，，垂足为G，若，则AE的边长为　　

    A. B. C. 4 D. 8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在△ABC中，AB=AC，D是△ABC外接圆劣弧AC上的点（不与A，C重合），延长BD至E．

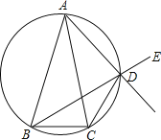
    （1）求证：AD的延长线平分∠CDE；

    （2）若∠BAC=30°，且△ABC底边BC边上高为1，求△ABC外接圆的周长．

    查看答案和解析>>

    同步练习册答案