
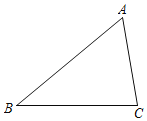
【题目】如图,已知△ABC,∠A=60°,AB=6,AC=4.
(1)用尺规作△ABC的外接圆O;
(2)求△ABC的外接圆O的半径;
(3)求扇形BOC的面积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)分别作出线段BC,线段AC的垂直平分线EF,MN交于点O,以O为圆心,OB为半径作⊙O即可.
(2)连接OB,OC,作CH⊥AB于H.解直角三角形求出BC,即可解决问题.
(3)利用扇形的面积公式计算即可.
(1)如图⊙O即为所求.
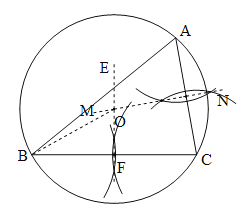
(2)连接OB,OC,作CH⊥AB于H.
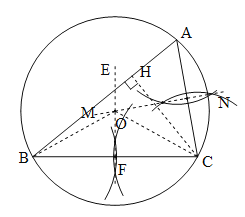
在Rt△ACH中,∵∠AHC=90°,AC=4,∠A=60°,
∴∠ACH=30°,
∴AH![]() AC=2,CH
AC=2,CH![]() AH=2
AH=2![]() ,
,
∵AB=6,
∴BH=4,
∴BC![]() 2
2![]() ,
,
∵∠BOC=2∠A=120°,OB=OC,OF⊥BC,
∴BF=CF![]() ,∠COF
,∠COF![]() ∠BOC=60°,
∠BOC=60°,
∴OC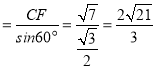 .
.
(3)S扇形OBC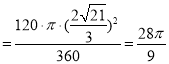 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
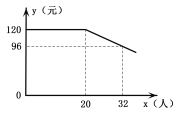
【题目】随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元).
(1)直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
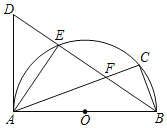
【题目】如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且DE=FE.
(1)求证:AD为⊙O切线;
(2)若AB=20,tan∠EBA=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第![]() 个图中正方形和等边三角形的个数之和为 个.
个图中正方形和等边三角形的个数之和为 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
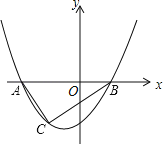
【题目】如图,二次函数y=ax2+bx+c的图象与x轴相交于A、B两点,C(m,﹣3)是图象上的一点,且AC⊥BC,则a的值为( )
A.2B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图1,直线BC及直线BC外一点P.
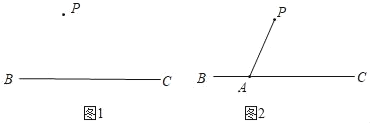
求作:直线PE,使得PE∥BC.
作法:如图2.
①在直线BC上取一点A,连接PA;
②作∠PAC的平分线AD;
③以点P为圆心,PA长为半径画弧,交射线AD于点E;
④作直线PE.
所以直线PE就是所求作的直线.根据小明设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵AD平分∠PAC,
∴∠PAD=∠CAD.
∵PA=PE,
∴∠PAD= ,
∴∠PEA= ,
∴PE∥BC.( )(填推理依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2+(m﹣3)x﹣3(m>0)与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,AB=4,点D为抛物线的顶点.
(1)求点A和顶点D的坐标;
(2)将点D向左平移4个单位长度,得到点E,求直线BE的表达式;
(3)若抛物线y=ax2﹣6与线段DE恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技有限公司用![]() 万元作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投人生产并进行销售.已知生产这种电子产品的成本为
万元作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投人生产并进行销售.已知生产这种电子产品的成本为![]() 元/件,在销售过程中发现:每年的年销售量
元/件,在销售过程中发现:每年的年销售量![]() (万件)与销售价格
(万件)与销售价格![]() (元/件)的关系如图所示,其中
(元/件)的关系如图所示,其中![]() 为反比例函数图象的一部分,
为反比例函数图象的一部分,![]() 为一次函数图象的一部分.设公司销售这种电子产品的年利润为
为一次函数图象的一部分.设公司销售这种电子产品的年利润为![]() (万元).(注意:第一年年利润=电子产品销售收人
(万元).(注意:第一年年利润=电子产品销售收人![]() 电子产品生产成本
电子产品生产成本![]() 研发费用)
研发费用)
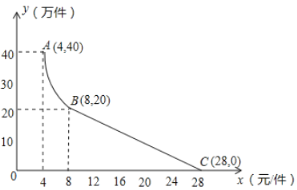
(1)分别写出图中![]() 段、
段、![]() 段
段![]() (万件)与
(万件)与![]() (元/件)之间的函数关系式,并写出自变量的取值范围;
(元/件)之间的函数关系式,并写出自变量的取值范围;
(2)求出第一年这种电子产品的年利润![]() (万元)与
(万元)与![]() (元/件)之间的函数关系式;
(元/件)之间的函数关系式;
(3)求该公司第一年年利润的最大值, 并说明利润最大时是盈利还是亏损,盈利或亏损多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com