
【题目】小明在学习了“等边三角形”后,激发了他的学习和探究的兴趣,就想考考他的朋友小崔,小明作了一个等边![]() ,如图1,并在边
,如图1,并在边![]() 上任意取了一点
上任意取了一点![]() (点
(点![]() 不与点
不与点![]() 、点
、点![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)若![]() ,求
,求![]() 的长度;
的长度;
(2)如图2,延长![]() 到
到![]() ,再延长
,再延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() ,
,![]() ,求证:
,求证:![]() .
.

【答案】(1)HI =5;(2)见解析.
【解析】
(1)作FP∥BC交AB于点P,证明![]() 是等边三角形得到AH=PH, 再证明
是等边三角形得到AH=PH, 再证明![]() 得到PI=BI,于是可得HI =
得到PI=BI,于是可得HI =![]() AB,即可求解;
AB,即可求解;
(2)延长BD至Q,使DQ=AB,连结EQ,就可以得出BE=BQ,得出△BEQ是等边三角形,就可以得出BE=QE,得出△BCE≌△QDE就可以得出结论.
解:如图1,作FP∥BC交AB于点P,

∵![]() 是等边三角形,
是等边三角形,
∴∠ABC=∠A=60°,
∵FP∥BC,
∴∠APF=∠ABC=60°, ∠PFI=∠BGI,
∴∠APF=∠A=60°,
∴![]() 是等边三角形,
是等边三角形,
∴PF=AF,
∵![]() ,
,
∴AH=PH,
∵AF=BG,
∴PF=BG,
∴在![]() 和
和![]() 中,
中,
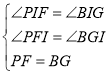 ,
,
∴![]() ,
,
∴PI=BI,
∴PI+PH=BI+AH=![]() AB,
AB,
∴HI=PI+PH =![]() AB=
AB= ![]() =5;
=5;
(2)如图2,延长BD至Q,使DQ=AB,连结EQ,
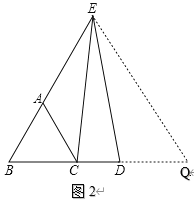
∵△ABC是等边三角形,
∴AB=BC=AC,∠B=60°.
∵AE=BD,DQ=AB,
∴AE+AB=BD+DQ,
∴BE=BQ.
∵∠B=60°,
∴△BEQ为等边三角形,
∴∠B=∠Q=60°,BE=QE.
∵DQ=AB,
∴BC=DQ.
∴在△BCE和△QDE中,
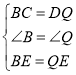 ,
,
∴△BCE≌△QDE(SAS),
∴EC=ED.
∴∠ECD=∠EDC.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
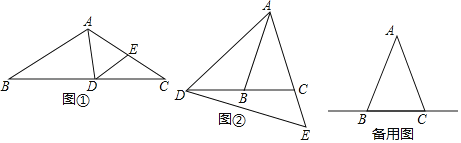
【题目】如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.
⑴如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;
⑵如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;
⑶当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校是乒乓球体育传统项目校,为进一步推动该项目的发展.学校准备到体育用品店购买甲、乙两种型号乒乓球若干个,已知3个甲种乒乓球和5个乙种乒乓球共需50元,2个甲种乒乓球和3个乙种乒乓球共需31元.
(1)求1个甲种乒乓球和1个乙种乒乓球的售价各是多少元?
(2)学校准备购买这两种型号的乒乓球共200个,要求甲种乒乓球的数量不超过乙种乒乓球的数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,
,![]() 与
与![]() 和
和![]() 分别相切于点
分别相切于点![]() 和点
和点![]() .点
.点![]() 和点
和点![]() 分别是
分别是![]() 和
和![]() 上的动点,
上的动点,![]() 沿
沿![]() 和
和![]() 平移.
平移.![]() 的半径为
的半径为![]() ,
,![]() .下列结论错误的是( )
.下列结论错误的是( )

A. ![]() B.
B. ![]() 和
和![]() 的距离为
的距离为![]()
C. 若![]() ,则
,则![]() 与
与![]() 相切 D. 若
相切 D. 若![]() 与
与![]() 相切,则
相切,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 内接于
内接于![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 的切线与
的切线与![]() 的延长线交于点
的延长线交于点![]() .
.

![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长;
的长;
![]() 在题设条件下,为使
在题设条件下,为使![]() 是平行四边形,
是平行四边形,![]() 应满足怎样的条件(不要求证明).
应满足怎样的条件(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O是斜边AB的中点,将边长足够大的三角板的直角顶点放在点O处,将三角板绕点O顺时针旋转一个角度α(0°<α<90°),记三角板的两直角边与Rt△ABC的两腰AC、BC的交点分别为E、D,四边形CEOD是旋转过程中三角板与△ABC的重叠部分(如图①所示).那么,在上述旋转过程中:

(1)线段CE与BD具有怎样的数量关系?四边形CEOD的面积是否发生变化?证明你发现的结论;
(2)当三角尺旋转角度为____________时,四边形CEOD是矩形;
(3)若三角尺继续旋转,当旋转角度α(90°<α<180°)时,三角尺的两边与等腰Rt△ABC的腰CB和AC的延长线分别交于点D、E(如图②所示). 那么线段CE与BD的数量关系还成立吗?若成立,给予证明;若不成立,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为5 厘米,对角线BD长8厘米.点P从点A出发沿AB方向匀速运动,速度为1厘米秒;点Q从点D 出发沿DB 方向匀速运动,速度为2 厘米/秒:P、Q 同时出发,当点Q与点B重合时,P、Q停止运动,设运动时间为t秒,解答下列问题:

(1)当t为何值时,△PBQ为等腰三角形?(2)当t为何值时,△PBQ的面积等于菱形ABCD面积的![]() ?
?
(3)连接AQ,在运动过程中,是否存在某一时刻t,使∠PQA=∠ABD?若存在,请求出t值; 若不存在,请说明理虫:
(4)直线PQ 交线段BC于点M,在运动过程中,是否存在某一时刻t,使BM:CM=2:3?若存在,请求出t值; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市里,某商户先后两次购进若干千克的黄瓜,第一次用了300元,第二次用了900元,但第二次的进货单价比第次的要高1.5元,而所购的黄瓜数量是第一次的2倍.
(1)问该商户两次一共购进了多少千克黄瓜?
(2)当商户按每千克6元的价格卖掉了![]() 时,商户想尽快卖掉这些黄瓜,于是商户决定将剩余的黄瓜打折销售,请你帮忙算算,剩余的黄瓜至少打几折才能使两次所进的黄瓜总盈利不低于360元?
时,商户想尽快卖掉这些黄瓜,于是商户决定将剩余的黄瓜打折销售,请你帮忙算算,剩余的黄瓜至少打几折才能使两次所进的黄瓜总盈利不低于360元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com