
 如图,矩形OABC在平面直角坐标系中,OA=2,∠BOC=30°,把△OBC沿OB对折,点C落在点D处,线段OD与AB交于点E.若点P在直线CD上,并且△OEP为直角三角形,求P点坐标.
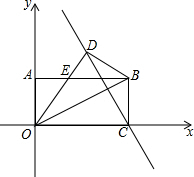
如图,矩形OABC在平面直角坐标系中,OA=2,∠BOC=30°,把△OBC沿OB对折,点C落在点D处,线段OD与AB交于点E.若点P在直线CD上,并且△OEP为直角三角形,求P点坐标. 分析 分三种情形讨论:①当∠EOP=90°时,PE2=PO2+OE2;②当∠OEP=90°时,OP2=OE2+EP2;③当∠OPE=90°时,OE2=EP2+OP2;分别列出方程解方程即可.
解答  解:如图,∵△OBD是由△OBC翻折,∠BOC=30°,∠AOC=90°,
解:如图,∵△OBD是由△OBC翻折,∠BOC=30°,∠AOC=90°,
∴∠BOC=∠BOD=∠AOE=30°,OD=OC,
∴△DOC是等边三角形,
在RT△AEO中,∵A0=2,∠OE=30°,
∴EA=$\frac{2\sqrt{3}}{3}$,点E坐标($\frac{2\sqrt{3}}{3}$,2),
在RT△BOC中,∵BC=AO=2,∠BOC=30°,
∴OC=2$\sqrt{3}$,∴点D坐标($\sqrt{3}$,3),点C坐标(2$\sqrt{3}$,0)
直线CD为y=-$\sqrt{3}$x+6,设点P(m,-$\sqrt{3}m+6$),
∴PO2=m2+(-$\sqrt{3}$m+6)2=4m2-12$\sqrt{3}$m+36,PE2=(m-$\frac{2\sqrt{3}}{3}$)2+(-$\sqrt{3}$m+4)2=4m2-$\frac{28\sqrt{3}}{3}$m+$\frac{52}{3}$,OE2=$\frac{16}{3}$,
①当∠EOP=90°时,PE2=PO2+OE2,4m2-$\frac{28\sqrt{3}}{3}$m+$\frac{52}{3}$=4m2-12$\sqrt{3}$m+36+$\frac{16}{3}$,解得m=3$\sqrt{3}$,∴点P坐标(3$\sqrt{3}$,-3);
②当∠OEP=90°时,OP2=OE2+EP2,4m2-12$\sqrt{3}$m+36=4m2-$\frac{28\sqrt{3}}{3}$m+$\frac{52}{3}$+$\frac{16}{3}$,解得m=$\frac{10\sqrt{3}}{9}$,∴点P坐标($\frac{10\sqrt{3}}{9}$,$\frac{8}{3}$);
③当∠OPE=90°时,OE2=EP2+OP2,方程无解.
综上所述,点P坐标为(3$\sqrt{3}$,-3)或($\frac{10\sqrt{3}}{9}$,$\frac{8}{3}$).
点评 本题考查翻折变换、坐标与图形的性质、矩形的性质、勾股定理等知识,学会分类讨论,用转化的思想去思考问题,计算量比较大.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
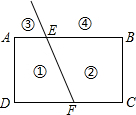 如图,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区城③④位于直线AB上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF的关系(不要求证明).
如图,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区城③④位于直线AB上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF的关系(不要求证明).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
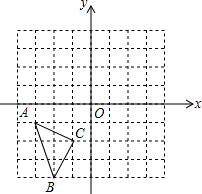 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标(-3,-1),
在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标(-3,-1),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
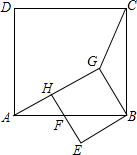 如图,在Rt△AGB中,∠AGB=90°,∠GAB=30°,以GB为边在GB的下方作正方形GBEH,以AB为边在AB的上方作正方形ABCD,连结CG.若FB=2,则CG2的值为15-6$\sqrt{3}$.
如图,在Rt△AGB中,∠AGB=90°,∠GAB=30°,以GB为边在GB的下方作正方形GBEH,以AB为边在AB的上方作正方形ABCD,连结CG.若FB=2,则CG2的值为15-6$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com