
【题目】如图,在平面直角坐标系中,正比例函数y=3x与反比例函数y=![]() 的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.
的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.

(1)求反比例函数的表达式;
(2)求△ABC的面积;
(3)若点P是反比例函数y=![]() 图象上的一点,△OPC与△ABC面积相等,请直接写出点P的坐标.
图象上的一点,△OPC与△ABC面积相等,请直接写出点P的坐标.
【答案】(1)y=![]() ;(2)S△ABC=12;(3)P点坐标为(1,12)或(﹣1,﹣12).
;(2)S△ABC=12;(3)P点坐标为(1,12)或(﹣1,﹣12).
【解析】
(1)把A点横坐标代入正比例函数可求得A点坐标,代入反比例函数解析式可求得k,可求得反比例函数解析式;
(2)根据反比例函数的对称性得出点B的坐标,再利用三角形的面积公式解答即可;
(3)由条件可求得B、C的坐标,可先求得△ABC的面积,再结合△OPC与△ABC的面积相等求得P点坐标.
解:(1)把x=2代入y=3x中,得y=2×3=6,
∴点A坐标为(2,6),
∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴k=2×6=12,
∴反比例函数的解析式为y=![]() ;
;
(2)∵AC⊥OC,
∴OC=2,
∵A、B关于原点对称,
∴B点坐标为(﹣2,﹣6),
∴B到OC的距离为6,
∴S△ABC=2S△ACO=2×![]() ×2×6=12,
×2×6=12,![]()
(3)∵S△ABC=12,
∴S△OPC=12,
设P点坐标为(x,![]() ),则P到OC的距离为|
),则P到OC的距离为|![]() |,
|,
∴![]() ×|
×|![]() |×2=12,解得x=1或﹣1,
|×2=12,解得x=1或﹣1,
∴P点坐标为(1,12)或(﹣1,﹣12).


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC的垂直平分线与对角线AC交于点O,与边AD、BC分别交于点E、F,那么四边形AFCE是不是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
让我们来规定一种运算:![]() ,
,
例如:![]() ,再如:
,再如:![]()
按照这种运算的规定:请解答下列各个问题:
①![]() ;
;
② 当![]() = 时,
= 时, ![]()
![]() =0;
=0;
③ 将下面式子进行因式分解: .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解学生到校交通方式情况,随机抽取各年级部分学生就“上下学交通方式”进行问卷调查,调查分为“A:骑自行车;B:步行;C:坐公交车;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图①)和部分扇形统计图(如图②),请根据图中的信息,解答下列问题.
(1)本次调查共抽取 名学生;
(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(3)若该中学共有学生3000人,估计有多少学生在上下学交通方式中选择坐公交车?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (1,0)和点
(1,0)和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() =1.
=1.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(2)连接![]() 、
、![]() ,若△
,若△![]() 的面积为6,求此抛物线的解析式;
的面积为6,求此抛物线的解析式;
(3)在(2)的条件下,点![]() 为
为![]() 轴正半轴上的一点,点
轴正半轴上的一点,点![]() 与点
与点![]() ,点
,点![]() 与点
与点![]() 关于点
关于点![]() 成中心对称,当△
成中心对称,当△![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两地相距240km,甲车先从A地出发30min后,乙车从B地出发,相向而行,甲车全程以80km/h的速度行驶,乙车以90km/h的速度行驶1h后,再以75kmh的速度驶完剩余路程,下列选项中能正确反映甲、乙两车距A地的距离y(km)与甲车行驶时间x(h)函数关系的图象是( )
A. 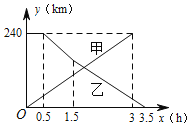 B.
B. 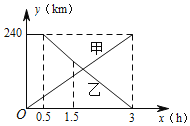
C. 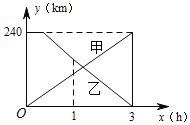 D.
D. 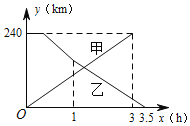
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A的坐标为A(-1,0).
(1)画出△ABC平移后得到的![]() 使得点A的对应点
使得点A的对应点![]() 的坐标为(2,-1),并写出
的坐标为(2,-1),并写出![]() 的坐标;
的坐标;
(2)画出△ABC绕点A顺时针旋转90°后得到的![]() 写出
写出![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织七年级学生参加了一次“运算能力”比赛,共有400名学生参加,参赛学生的成![]() 均为正数,且最低分为60分,为了解本次比赛学生的成绩分布情况,抽取了其中部分学生的成绩作为样本进行统计,并制作出了如下两个统计图:
均为正数,且最低分为60分,为了解本次比赛学生的成绩分布情况,抽取了其中部分学生的成绩作为样本进行统计,并制作出了如下两个统计图:
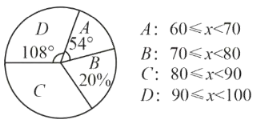
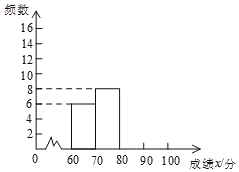
请根据所给信息,解答下列问题:
(1)所抽取分析的学生数量为 人;
(2)成绩为![]() 这一组的人数占体体人数的百分比为 ;
这一组的人数占体体人数的百分比为 ;
(3)成绩为![]() 这一组的所在的扇形的圆心角度数为 ;
这一组的所在的扇形的圆心角度数为 ;
(4)请补全频数分布直方图;
(5)若成绩达到90分或以上为“优秀”等级,则参加这次比赛的学生中属于“优秀”等级的约有 人 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com