
【题目】在Rt△POQ中,OP=OQ=4,M是PQ中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB;

【答案】证明见解析.
【解析】
试题过点M作ME⊥OP于点E,作MF⊥OQ于点F,可得四边形OEBF是矩形,根据三角形的中位线定理可得ME=MF,再根据同角的余角相等可得∠AME=∠BMF,再利用“角边角”证明△AME和△BMF全等,根据全等三角形对应边相等即可证明.
试题解析:证明:如图,过点M作ME⊥OP于点E,作MF⊥OQ于点F,

∵∠O=90°,
∴四边形OEMF是矩形,
∵M是PQ的中点,OP=OQ=4,∠O=90°,
∴ME=![]() OQ=2,MF=
OQ=2,MF=![]() OP=2,
OP=2,
∴ME=MF,
∴四边形OEMF是正方形,
∵∠AME+∠AMF=90°,∠BMF+∠AMF=90°,
∴∠AME=∠BMF,
在△AME和△BMF中,
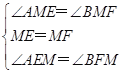 ,
,
∴△AME≌△BMF(ASA),
∴MA=MB;
考点: 1.旋转的性质;2.全等三角形的判定与性质;3.等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图所示在三角形△ABC中AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,则下列四个结论中,①AB上一点与AC上一点到D的距离相等;②AD上任意一点到AB、AC的距离相等;③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的个数是
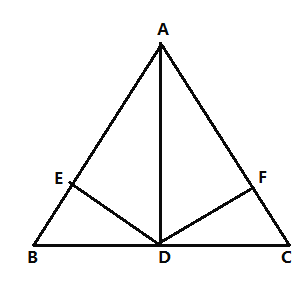
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米。一只小虫在长方体表面从A爬到B的最短路程是__________
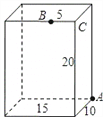
查看答案和解析>>
科目:初中数学 来源: 题型:
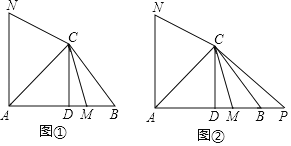
【题目】在△ABC中,∠BAC=45°,CD⊥AB,垂足为点D,M为线段DB上一动点(不包括端点),点N在直线AC左上方且∠NCM=135°,CN=CM,如图①.
(1)求证:∠ACN=∠AMC;
(2)记△ANC得面积为5,记△ABC得面积为5.求证:![]() ;
;
(3)延长线段AB到点P,使BP=BM,如图②.探究线段AC与线段DB满足什么数量关系时对于满足条件的任意点M,AN=CP始终成立?(写出探究过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2 - 2(1-m)x+m2的两实数根为x1,x2.
(1)求m的取值范围;
(2)设![]() ,当m为何值时,y有最小值,求y的最小值.
,当m为何值时,y有最小值,求y的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,则下列五个结论中:①albic<0;②a﹣b+c>0;③2a﹣b<0;④abc<0;⑤4a+2b+c>0,错误的个数有( )
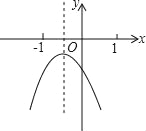
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】情境观察:
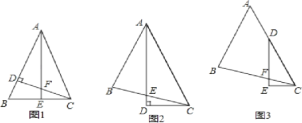
如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com