
 如图所示,直线EF上有两点A,C,分别引两条射线AB,CD,∠BAF=110°,∠DCF=60°,射线AB,CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t,在射线CD移动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.
如图所示,直线EF上有两点A,C,分别引两条射线AB,CD,∠BAF=110°,∠DCF=60°,射线AB,CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t,在射线CD移动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.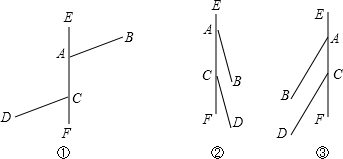 解:存在.分三种情况:
解:存在.分三种情况:

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图所示,九年级某兴趣小组要测量校园内的教学楼AB的高度,在地面上C点用测角仪测得楼顶A点的仰角∠AFE=60°,再沿着直线BC后退8m到达点D,在D点又测得楼顶A的仰角∠AGE=45°,已知测角仪的高度CF为1.6m.求教学楼AB的高度.(结果保留小数点后一位,
如图所示,九年级某兴趣小组要测量校园内的教学楼AB的高度,在地面上C点用测角仪测得楼顶A点的仰角∠AFE=60°,再沿着直线BC后退8m到达点D,在D点又测得楼顶A的仰角∠AGE=45°,已知测角仪的高度CF为1.6m.求教学楼AB的高度.(结果保留小数点后一位,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
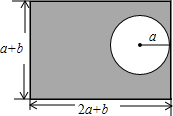 某个居民小区的长方形花园的长、宽分别为2a+b和a+b,中间有一个半径为a的圆形游乐场(如图),请你用代数式表示图中阴影部分的面积,再求当a=5米,b=10米时阴影部分面积(π取3.14).
某个居民小区的长方形花园的长、宽分别为2a+b和a+b,中间有一个半径为a的圆形游乐场(如图),请你用代数式表示图中阴影部分的面积,再求当a=5米,b=10米时阴影部分面积(π取3.14).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com