
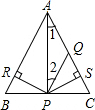
 如图,△ABC中,∠1=∠2,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论:①AS=AR;②QP∥AB;③△BRP≌△QSP,( )
如图,△ABC中,∠1=∠2,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论:①AS=AR;②QP∥AB;③△BRP≌△QSP,( )| A、全部正确 | B、①和②正确 |
| C、仅①正确 | D、①和③正确 |
|


科目:初中数学 来源: 题型:
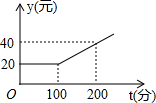 已知甲、乙两家通信公司都推出了市话通话优惠业务,甲公司每月的市话费标准如图所示,乙公司每月通话收费标准如表所示.
已知甲、乙两家通信公司都推出了市话通话优惠业务,甲公司每月的市话费标准如图所示,乙公司每月通话收费标准如表所示.| 月租费 | 通话费 |
| 25元 | 0.15元/分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:
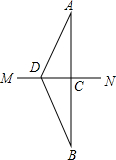 如图,A、B两个村庄在河MN的两侧,连接AB,与MN相交于点C,点D在MN上,连接AD、BD,且AD=BD,若要在河上建一座桥,使A、B两村来往最便捷,则应该把桥建在点C还是点D?为什么?
如图,A、B两个村庄在河MN的两侧,连接AB,与MN相交于点C,点D在MN上,连接AD、BD,且AD=BD,若要在河上建一座桥,使A、B两村来往最便捷,则应该把桥建在点C还是点D?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com