
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离cm. 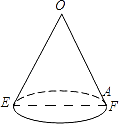
【答案】2 ![]()
【解析】解:因为OE=OF=EF=10(cm), 所以底面周长=10π(cm),
将圆锥侧面沿OF剪开展平得一扇形,此扇形的半径OE=10(cm),弧长等于圆锥底面圆的周长10π(cm)
设扇形圆心角度数为n,则根据弧长公式得:
10π= ![]() ,
,
所以n=180°,
即展开图是一个半圆,
因为E点是展开图弧的中点,
所以∠EOF=90°,
连接EA,则EA就是蚂蚁爬行的最短距离,
在Rt△AOE中由勾股定理得,
EA2=OE2+OA2=100+64=164,
所以EA=2 ![]() (cm),
(cm),
即蚂蚁爬行的最短距离是2 ![]() (cm).
(cm).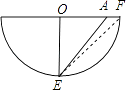
要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究:如图1,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=40°,求∠DEF的度数.
(2)应用:如图2,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB的延长线上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=60°,求∠DEF的度数.
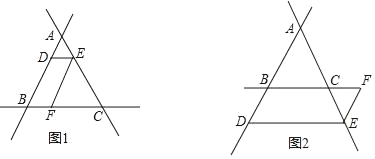
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乌苏市某生态示范园,计划种植一批苹果梨,原计划总产量达36万千克,为了满足市场需求,现决定改良苹果梨品种,改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万千克,种植亩数减少了20亩,则原计划和改良后平均每亩产量各多少万千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC=4,BD=6,P是BD上的任一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E、F,设BP=x,EF=y,则能反映y与x之间关系的图象是( ) 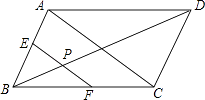
A.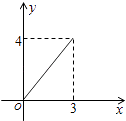
B.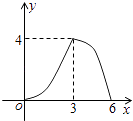
C.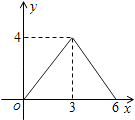
D.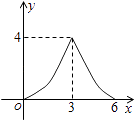
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求值:1+2+22+23+24++22013.
解:设S=1+2+22+23+24+…+22013.将等式两边同时乘以2,得
2S=2+22+23+24+…+22013+22014
将下式减去上式,得2S﹣S=22014﹣1.
即S=1+2+22+23+24++22013=22014﹣1.
请你仿照此法计算1+3+32+33+34+…+32018的值是( )
A. 32018﹣1 B. ![]() C. 32019﹣1 D.
C. 32019﹣1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在300米环形跑道上练习长跑,甲的速度是6米/秒,乙的速度是7米/秒.
(1)如果甲、乙两人同地背向跑,乙先跑2秒,再经过多少秒两人相遇?
(2)如果甲、乙两人同地同向跑,乙跑几圈后能首次追上甲?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( ) 
A.102°
B.112°
C.115°
D.118°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
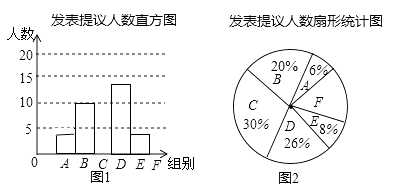
(1)求得样本容量为 , 并补全直方图;
(2)如果会议期间组织1700名代表参会,请估计在这一天里发言次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com