
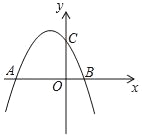
【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣![]() x2+bx+c与x轴交于点A(﹣3,0)和点B,与y轴交于点C (0,2).
x2+bx+c与x轴交于点A(﹣3,0)和点B,与y轴交于点C (0,2).
(1)求抛物线的表达式,并用配方法求出顶点D的坐标;
(2)若点E是点C关于抛物线对称轴的对称点,求tan∠CEB的值.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() +2,顶点D的坐标为(﹣1,
+2,顶点D的坐标为(﹣1,![]() );(2)tan∠CEB的值是
);(2)tan∠CEB的值是![]() .
.
【解析】
(1)∵抛物线y=﹣![]() x2+bx+c与x轴交于点A(﹣3,0)和点B,与y轴交于点C (0,2),
x2+bx+c与x轴交于点A(﹣3,0)和点B,与y轴交于点C (0,2),
∴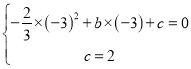 ,
,
得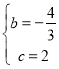 ,
,
∴y=﹣![]() x2﹣
x2﹣![]() x+2=
x+2=![]() ,
,
∴抛物线顶点D的坐标为(﹣1,![]() ),
),
即该抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+2,顶点D的坐标为(﹣1,
x+2,顶点D的坐标为(﹣1,![]() );
);
(2)∵y=![]() ,
,
∴该抛物线的对称轴为直线x=﹣1,
∵点E是点C关于抛物线对称轴的对称点,点C(0,2),
∴点E的坐标为(﹣2,2),
当y=0时,0=![]() ,得x1=﹣3,x2=1,
,得x1=﹣3,x2=1,
∴点B的坐标为(1,0),
设直线BE的函数解析式为y=kx+n,
![]() ,得
,得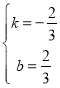 ,
,
∴直线BE的函数解析式为y=﹣![]() +
+![]() ,
,
当x=0时,y=![]() ,
,
设直线BE与y轴交于点F,则点F的坐标为(0,![]() ),
),
∴OF=![]() ,
,
∵点C(0,2),点E(﹣2,2),
∴OC=2,CE=2,
∴CF=2﹣![]() =
=![]() ,
,
∴tan∠CEF=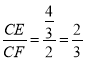 ,
,
即tan∠CEB的值是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB是![]() 的直径,C点在
的直径,C点在![]() 上,连接AC,
上,连接AC,![]() 的平分线交
的平分线交![]() 于点D,过点D作
于点D,过点D作![]() 交AC的延长线于点E.
交AC的延长线于点E.
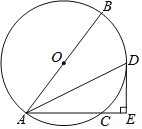
(1)求证:DE是![]() 的切线;
的切线;
(2)若AB=10,![]() ,连接CD,求CD的长.
,连接CD,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,![]() 的顶点坐标分别是
的顶点坐标分别是![]() ,对于
,对于![]() 的横长、纵长、纵横比给出如下定义:
的横长、纵长、纵横比给出如下定义:
将![]() 中的最大值,称为
中的最大值,称为![]() 的横长,记作
的横长,记作![]() ;将
;将![]() 中的最大值,称为
中的最大值,称为![]() 的纵长,记作
的纵长,记作![]() ;将
;将![]() 叫做
叫做![]() 的纵横比,记作
的纵横比,记作![]() .
.
例如:如图![]() 的三个顶点的坐标分别是
的三个顶点的坐标分别是![]() ,则
,则![]() ,
,
所以![]() .
.
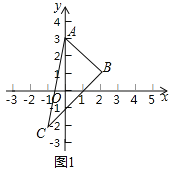
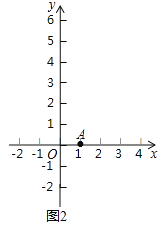
![]() 如图2,点
如图2,点![]() ,
,
![]() 点
点![]() ,
,
则![]() 的纵横比
的纵横比![]() ______
______
![]() 的纵横比
的纵横比![]() ______;
______;
![]() 点F在第四象限,若
点F在第四象限,若![]() 的纵横比为1,写出一个符合条件的点F的坐标;
的纵横比为1,写出一个符合条件的点F的坐标;
![]() 点M是双曲线
点M是双曲线![]() 上一个动点,若
上一个动点,若![]() 的纵横比为1,求点M的坐标;
的纵横比为1,求点M的坐标;
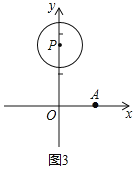
![]() 如图3,点
如图3,点![]() 以
以![]() 为圆心,1为半径,点N是
为圆心,1为半径,点N是![]() 上一个动点,直接写出
上一个动点,直接写出![]() 的纵横比
的纵横比![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,DE 是⊙O的切线,连结OD,OE
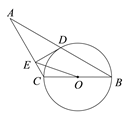
(1)求证:∠DEA=90°;
(2)若BC=4,写出求 △OEC的面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
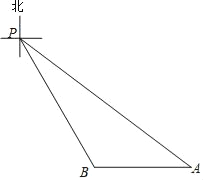
【题目】如图,P点是某海域内的一座灯塔的位置,船A停泊在灯塔P的南偏东53°方向的50海里处,船B位于船A的正西方向且与灯塔P相距20![]() 海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
(1)试问船B在灯塔P的什么方向?
(2)求两船相距多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
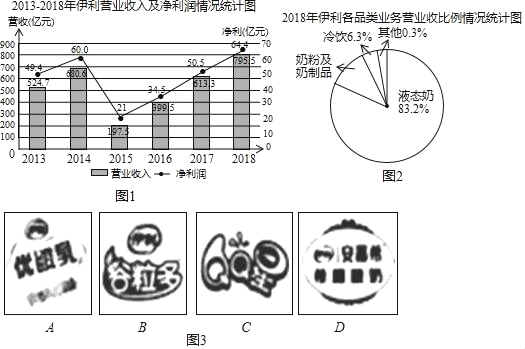
【题目】伊利集团是中国规模最大、产品线最全的乳制品企业.综合实践小组的同学从网上搜集到如下一些伊利集团近几年的营业状况的资料,其中图1是2013﹣2018年伊利集团营业收入及净利润情况统计图,图2是2018年伊利集团各品类业务营收比例情况统计图(数据来源:公司财报、中商产业研究院).
(1)解读信息:
综合实践小组的同学结合统计图提出了如下问题,请你解答:
①2018年,伊利集团营收及净利再次刷新行业纪录,稳居亚洲乳业第一.这一年,伊利集团实现营业收人 亿元,净利润 亿元;
②求2018年伊利集团“奶粉及奶制品“业务的营业收入(结果保留整数);
③在2013﹣2018这6年中;伊利集团净利润比上一年增长额最多的是 年;估计2019年伊利集团的净利润将比上一年增长 亿元,理由是 ;
(2)拓展活动:
如图,同学们收集了伊利集团旗下“优酸乳、谷粒多、QQ星,安幕希”四种产品的商标图片(四张图片除商标图案外完全相同,分别记为A,B,C,D)(见图3).同学们用这四张卡片设计了一个游戏,规则是:将四张图片背面朝上放在桌上,搅匀后,由甲从中随机抽取一张,记下商标名称后放回;再次搅匀后,由乙从中随机抽取一张.若两人抽到的商标相同则甲获胜;否则,乙获胜,这个规则对甲乙双方公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
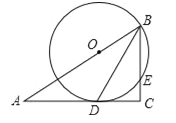
【题目】如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AB=5cm,点M在AB上且AM=1cm,点P是半圆O上的动点,过点B作BQ⊥PM交PM(或PM的延长线)于点Q.设PM=xcm,BQ=ycm.(当点P与点A或点B重合时,y的值为0)小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:

(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 0 | 3.7 | ______ | 3.8 | 3.3 | 2.5 | ______ |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BQ与直径AB所夹的锐角为60°时,PM的长度约为______cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com