
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.
求证:AM=AN.

【答案】证明见解析
【解析】证明:∵△AEB由△ADC旋转而得,∴△AEB≌△ADC。∴∠EAB=∠CAD,∠EBA=∠C。
∵AB=AC,AD⊥BC,∴∠BAD=∠CAD,∠ABC=∠C。
∴∠EAB=∠DAB,∠EBA=∠DBA。
∵∠EBM=∠DBN,∴∠MBA=∠NBA。
又∵AB=AB,∴△AMB≌△ANB(ASA)。∴AM=AN。
根据旋转的性质可得△AEB≌△ADC,根据全等三角形对应角相等可得∠EAB=∠CAD,∠EBA=∠C,结合等腰三角形三线合一的性质即可推出∠EAB=∠DAB,∠EBA=∠DBA,从而推出∠MBA=∠NBA,然后根据“角边角”证明△AMB≌△ANB,根据全等三角形对应边相等即可得证。


科目:初中数学 来源: 题型:
【题目】如图1所示,称“对顶三角形”,其中,∠A+∠B=∠C+∠D
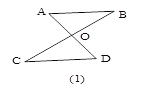

利用这个结论,完成下列填空.
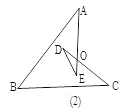
(1)如图 (2),∠A+∠B+∠C+∠D+∠E= ;
(2)如图(3),∠A+∠B+∠C+∠D+∠E= ;
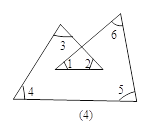
(3)如图(4),∠1+∠2+∠3+∠4+∠5+∠6= ;
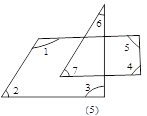
(4)如图(5),∠1+∠2+∠3+∠4+∠5+∠6+∠7= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的个数有( )
①三点确定一个圆;②平分弦的直径垂直于弦;③三角形的外心到三角形三边的距离相等;④等弧所对的圆周角相等;⑤以![]() 、
、![]() 、
、![]() 为边的三角形,其内切圆的半径是
为边的三角形,其内切圆的半径是![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第十五届中国“西博会”已于![]() 年
年![]() 月底在成都召开,现有
月底在成都召开,现有![]() 名志愿者准备参加某分会场的工作,其中男生
名志愿者准备参加某分会场的工作,其中男生![]() 人,女生
人,女生![]() 人.
人.
(1)若从这![]() 人中随机选取一人作为联络员,求选到女生的概率;
人中随机选取一人作为联络员,求选到女生的概率;
(2)若该分会场的某项工作只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为![]() 、
、![]() 、
、![]() 、
、![]() 的扑克牌洗匀后,数字朝下放于桌面,从中任取
的扑克牌洗匀后,数字朝下放于桌面,从中任取![]() 张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.
张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系网格中,格点A的位置如图所示:

(1)若点B坐标为(2,3),请你画出△AOB;
(2)若△AOB与△A′O′B′关于y轴对称,请你画出△A′O′B';
(3)请直接写出线段AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过![]() 的集中药物喷洒,再封闭宿舍
的集中药物喷洒,再封闭宿舍![]() ,然后打开门窗进行通风,室内每立方米空气中含药量
,然后打开门窗进行通风,室内每立方米空气中含药量![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
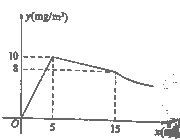
A. 经过![]() 集中喷洒药物,室内空气中的含药量最高达到
集中喷洒药物,室内空气中的含药量最高达到![]()
B. 室内空气中的含药量不低于![]() 的持续时间达到了
的持续时间达到了![]()
C. 当室内空气中的含药量不低于![]() 且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D. 当室内空气中的含药量低于![]() 时,对人体才是安全的,所以从室内空气中的含药量达到
时,对人体才是安全的,所以从室内空气中的含药量达到![]() 开始,需经过
开始,需经过![]() 后,学生才能进入室内
后,学生才能进入室内
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点 B、O分别落在点 B1、C1 处,点B1在x轴上,再将△AB1C1 绕点 B1 顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2 绕点C2 顺时针旋转到△A2B2C2 的位置,点 A2 在x轴上,依次进行下去….若点 A(![]() ,0),B(0,4),则点 B2016 的横坐标为_______.
,0),B(0,4),则点 B2016 的横坐标为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com