练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，矩形ABCD中，点E在DC上且DE：EC＝2：3，连接BE交对角线AC于点O．延长AD交BE的延长线于点F，则△AOF与△BOC的面积之比为（　　）

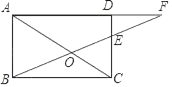
    A. 9：4B. 3：2C. 25：9D. 16：9

    【答案】C

    【解析】

    由矩形的性质可知：AB＝CD，AB∥CD，进而可证明△AOB∽△COE，结合已知条件可得AO：OC＝3：5，再根据相似三角形的性质：面积之比等于相似比的平方即可求出△AOF与△BOC的面积之比．

    解：∵四边形ABCD是矩形，

    ∴AB＝CD，AB∥CD，

    ∴△AOB∽△COE，

    ∵DE：EC＝2：3，

    ∴CE：CD＝3：5，

    ∴CE：CD＝CE：AB=CO:AO＝3：5，

    ∴S△AOF：S△BOC＝25：9．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

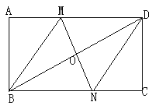
    【题目】如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点N，连接BM，DN.

    （1）求证：四边形BMDN是菱形；

    （2）若AB=4，AD=8，求MD的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】星期五晚上，小明和他的妈妈一起看《歌手》，歌手演唱完后要评选出名次，在已公布四到七名后，还有华晨宇、汪峰、张韶涵三位选手没有公布名次.

    （1）求汪峰获第一名的概率;

    （2）如果小明和妈妈一起竞猜第一名，那么两人中一个人猜中另一个人却没猜中的概率是多少？（请用“树状图”或“列表”等方法写出分析过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，用三种大小不同的五个正方形和一个缺角的长方形拼成长方形 ABCD，其中，NH=NG 1cm ，设 BF acm ．

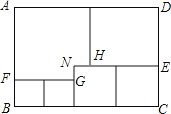
    （1）用含 a 的代数式分别表示 CE，DE；

    （2）求长方形 ABCD 的周长．（用含 a 的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，四边形OABC为矩形，A（6，0），C（0，3），点M在边OA上，且M（4，0），P、Q两点同时从点M出发，点P沿x轴向右运动；点Q沿x轴先向左运动至原点O后，再向右运动到点M停止，点P随之停止运动．P、Q两点运动的速度分别为每秒1个单位、每秒2个单位．以PQ为一边向上作正方形PRLQ．设点P的运动时间为t（秒），正方形PRLQ与矩形OABC重叠部分（阴影部分）的面积为S（平方单位）．

    （1）用含t的代数式表示点P的坐标．

    （2）分别求当t=1，t=3时，线段PQ的长．

    （3）求S与t之间的函数关系式．

    （4）直接写出L落在第一象限的角平分线上时t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是按照一定规律画出的“树形图”，经观察可以发现：图A2比图A1多出2个“树枝”，图A3比图A2多出4个“树枝”，图A4比图A3多出8个“树枝”……照此规律，图A6比图A2多出“树枝”( )

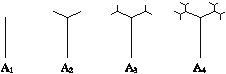
    A.32个B.56个C.60个D.64个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）图（1）是一个长为2m，宽为2n的矩形，把此矩形沿图中虚线用剪刀均分为四个小长方形，然后按图（2）的形状拼成一个大正方形．请问：这两个图形的什么量不变？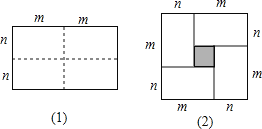

    （2）把所得的大正方形面积比原矩形的面积多出的阴影部分的面积用含m，n的代数式表示为（m-n）2或m2-2mn+n2 ．
    （3）由前面的探索可得出的结论是：在周长一定的矩形中，当 时，面积最大．
    （4）若矩形的周长为24cm，则当边长为多少时，该图形的面积最大？最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读计算：

    阅读下列各式：，，……

    回答下列三个问题：

    （1）验证：（5×0.2）10=__________；510×0.210=__________．

    （2）通过上述验证，归纳得出： =__________；=__________．

    （3）请应用上述性质计算：

    ①

    ②．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

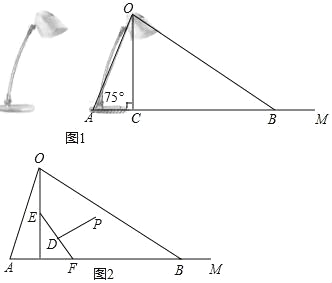
    【题目】如图1为放置在水平桌面上的台灯的平面示意图，灯臂AO长为50cm，与水平桌面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平桌面所形成的夹角∠OCA，∠OBA分别为90°和30°．（不考虑其他因素，结果精确到0.1cm． sin75°≈0.97，cos75°≈0.26，≈1.73

    （1）求该台灯照亮水平桌面的宽度BC．

    （2）人在此台灯下看书，将其侧面抽象成如图2所示的几何图形，若书与水平桌面的夹角∠EFC为60°，书的长度EF为24cm，点P为眼睛所在位置，当点P在EF 的垂直平分线上，且到EF距离约为34cm（人的正确看书姿势是眼睛离书距离约1尺≈34cm）时，称点P为“最佳视点”．请通过计算说明最佳视点P在不在灯光照射范围内？

    查看答案和解析>>

    同步练习册答案