
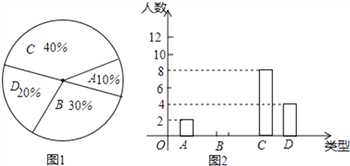
����Ŀ��ijУҪ��200��ѧ�����������飬ÿ�˱������3~6�ݱ��棬�����������������20��ѧ��ÿ����ɱ���ķ���������Ϊ���࣬A��3�ݣ�B��4�ݣ�C��5�ݣ�D��6�ݣ���������������Ƴ�����ͼ����ͼ1������δ����������ͼ����ͼ2�����ش��������⣺
��1���뽫����ͳ��ͼ2����������
��2��д����20��ѧ��ÿ����ɱ������������_____�ݺ���λ��_____�ݣ�
��3�������20��ѧ��ÿ����ɱ��������ƽ����ʱ��С�������������ģ�
��һ������ƽ�����Ĺ�ʽ�� ![]() =
=![]() ��
��
�ڶ������ڸ������У�n=4��x1=3��x2=4��x3=5��x4=6��
��������![]() =
=![]() =4.5���ݣ�.
=4.5���ݣ�.
С���ķ����Բ��ԣ�����ԣ���˵�����ɣ�������ԣ��������ȷ�����
��4���ִӡ�D�ࡱ��ѧ�������ѡ��2�˽��вɷã�����D�ࡱ��ѧ����ֻ��1������������ѡ��λͬѧ������ͬѧ�ĸ����Ƕ��٣������б�������״ͼ�ķ�����⣮
���𰸡���1������������2��5,5����3������������4��![]() ��
��
��������������(1)B����������ڵ������������30%��(2)�����ڰ�������λ���Ķ�����⣻(3)ƽ�����������ݵ��ܺͳ��Ե����������(4)���б�������״ͼ�ķ������.
��⣺(1)�����������20��30%��6��.
����ͳ��ͼ2�������£�
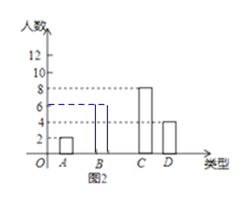
(2)������������λ���Ķ���ã�������5����λ����5��
(3)���ԣ���ȷ���Ϊ![]() ��
��
(4)�ִӡ�D�ࡱ��ѧ�������ѡ��2�˽��вɷã�����D�ࡱ��ѧ����ֻ��1������������ѡ��λͬѧ������ͬѧ�ĸ����Ƕ��٣������б�������״ͼ�ķ�����⣮
�⣺�衰D�ࡱѧ���ı��Ϊ1��2��3��4������1��ѧ��Ϊ�������б����£�
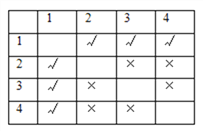
�ɱ����֪�����еȿ��ܵĽ��Ϊ12�֣�����ͬѧ�Ľ��Ϊ6�֣���P(����ͬѧ)��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
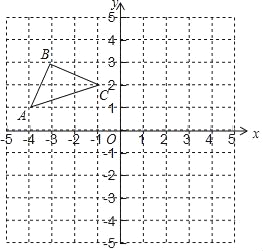
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��֪��ABC������������ֱ�ΪA����4��1����B����3��3����C����1��2����
��1��������ABC����x��ԳƵġ�A1B1C1����A��B��C�ĶԳƵ�ֱ��ǵ�A1��B1��C1��ֱ��д����A1��B1��C1�����꣺A1���� ������ ������B1���� ������ ������C1���� ������ ������
��2��������C����y��ĶԳƵ�C2������C1C2��CC2��C1C����ֱ��д����CC1C2��������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB=AC����A=36����AB�Ĵ�ֱƽ���߽�AC��D�������н��ۣ��١�C=72������BD�ǡ�ABC��ƽ���ߣ��ۡ�ABD�ǵ��������Σ��ܡ�BCD�ǵ��������Σ�������ȷ����____
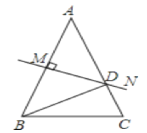
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O=30�㣬��B��OM���ϵ�һ�����Դ���ڱ�ON�Ϸ�һƽ�澵������BC��
��ƽ�澵�������������OM�Ľ����ΪE�����OCE�ǵ��������εĸ����У� ��
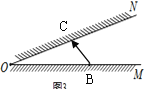
A. 1�� B. 2�� C. 3�� D. 3������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
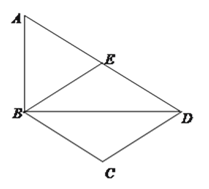
����Ŀ����ͼ����Rt��ABD�У���ABD=90�㣬AB=1��sin��ADB=![]() ����EΪAD���е㣬�߶�BA�Ƶ�B˳ʱ����ת��BC����ת��С��180�㣩��ʹBC��AD������DC��BE��
����EΪAD���е㣬�߶�BA�Ƶ�B˳ʱ����ת��BC����ת��С��180�㣩��ʹBC��AD������DC��BE��
��1�����ı���BCDE��________����֤����Ľ��ۣ�
��2�����߶�AB��ת������ɨ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������ͣ���������⣬ij��λ�⽨�����ͣ���⣬�������ʦ�ṩ�˸õ���ͣ��������ʾ��ͼ�����涨������ͣ�����µ����Ϸ�Ҫ�����߱�־���Ա��֪ͣ���˳����ܷ�ȫʻ�롣(����AB=9m��BC=0.5m)Ϊ�����ߣ�������ݸ�ͼ����CE��(��ȷ��0.1m)���ο���ֵ![]() ��
��![]() ��
��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̩�ݳ���K����ͷ�г�A����T����ͷ�г�B����ֱ���Ͼ�����֪A����ƽ���ٶ�Ϊ80 km/h��B����ƽ���ٶ�ΪA����1.5����������ȫ��B������ʱ���A����40���ӣ�
(1)��̩�����Ͼ�����·��̣�
(2)�������Ը��Ե�ƽ���ٶȷֱ��̩�ݡ��Ͼ�ͬʱ������У��ʾ�������ʱ���������40 km?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
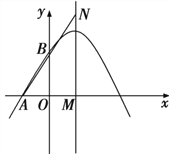
����Ŀ����ͼ��������![]() ��
��![]() ���㣮
���㣮
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() Ϊ�����߶Գ�����x��Ľ��㣬NΪ�Գ�����һ�㣬��
Ϊ�����߶Գ�����x��Ľ��㣬NΪ�Գ�����һ�㣬��![]() ����M��AN�ľ��룮
����M��AN�ľ��룮
![]() �������ߵĶԳ������Ƿ���ڵ�P��ʹ
�������ߵĶԳ������Ƿ���ڵ�P��ʹ![]() Ϊ���������Σ������ڣ���ֱ��д�����������ĵ�
Ϊ���������Σ������ڣ���ֱ��д�����������ĵ�
P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
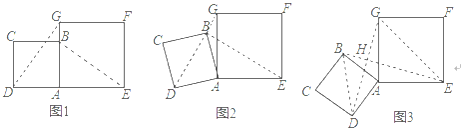
����Ŀ������ѧ��ȤС���У�С�����߳�Ϊ2��������![]() ��߳�Ϊ
��߳�Ϊ![]() ��������
��������![]() ����ͼ1��ʽ���ã�
����ͼ1��ʽ���ã�![]() ��
��![]() ��ͬһ��ֱ���ϣ�
��ͬһ��ֱ���ϣ�![]() ��
��![]() ��ͬһ��ֱ���ϣ�
��ͬһ��ֱ���ϣ�
��1���������![]() ��
��![]() ֮���������λ�ù�ϵ��������֤����
֮���������λ�ù�ϵ��������֤����
��2����ͼ2�У�����������![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת������
��ʱ����ת������![]() ǡ�������߶�
ǡ�������߶�![]() ��ʱ�����
��ʱ�����![]() �ij���
�ij���
��3����ͼ3�У�����������![]() �Ƶ�
�Ƶ�![]() ������ʱ����ת�����߶�
������ʱ����ת�����߶�![]() ���߶�
���߶�![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��д��
���![]() ��
��![]() ���֮�͵����ֵ������Ҫ˵�����ɣ�
���֮�͵����ֵ������Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com