
【题目】求证:相似三角形对应角的角平分线之比等于相似比.
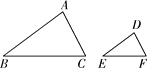
要求:①分别在给出的相似三角形△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
【答案】①见解析;②见解析
【解析】
①按照角平分线的作法分别作出一组对应角的平分线即可;
②先根据△ABC∽△DEF得出∠BAC=∠EDF,∠B=∠E,进而可证△ABG∽△DEH,根据相似三角形的性质有![]() ,则结论可证.
,则结论可证.
解:①如解图所示,AG,DH分别是∠BAC与∠EDF的角平分线;

②已知:如解图,△ABC∽△DEF,![]() =
=![]() =
=![]() =k,AG,DH分别是∠BAC与∠EDF的角平分线.
=k,AG,DH分别是∠BAC与∠EDF的角平分线.
求证:![]() =k.
=k.
证明:∵AG,DH分别是∠BAC与∠EDF的角平分线,
∴∠BAG=![]() ∠BAC,∠EDH=
∠BAC,∠EDH=![]() ∠EDF.
∠EDF.
∵△ABC∽△DEF,
∴∠BAC=∠EDF,∠B=∠E.
∴∠BAG=∠EDH.
∴△ABG∽△DEH.
∴![]() =
=![]() =k.
=k.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】某高中进行“选科走班”教学改革,语文、数学、英语三门为必修学科,另外还需从物理、化学、生物、政治、历史、地理(分别记为A、B、C、D、E、F)六门选修学科中任选三门,现对该校某班选科情况进行调查,对调查结果进行了分析统计,并制作了两幅不完整的统计图.
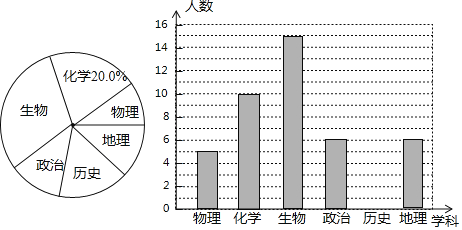
请根据以上信息,完成下列问题:
(1)该班共有学生人;
(2)请将条形统计图补充完整;
(3)该班某同学物理成绩特别优异,已经从选修学科中选定物理,还需从余下选修学科中任意选择两门,请用列表或画树状图的方法,求出该同学恰好选中化学、历史两科的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
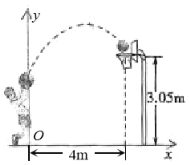
【题目】如图,一位篮球运动员在离篮圈水平距离4![]() 处跳起投篮,球运行的高度
处跳起投篮,球运行的高度![]() (
(![]() )与运行的水平距离
)与运行的水平距离![]() (
(![]() )满足解析式
)满足解析式![]() ,当球运行的水平距离为1.5
,当球运行的水平距离为1.5![]() 时,球离地面高度为3.3
时,球离地面高度为3.3![]() ,球在空中达到最大高度后,准确落入篮圈内.已知篮圈中心离地面距离为3.05
,球在空中达到最大高度后,准确落入篮圈内.已知篮圈中心离地面距离为3.05![]() .
.
(1)当球运行的水平距离为多少时,达到最大高度?最大高度为多少?
(2)若该运动员身高1.8![]() ,这次跳投时,球在他头顶上方0.25
,这次跳投时,球在他头顶上方0.25![]() 处出手,问球出手时,他跳离地面多高?
处出手,问球出手时,他跳离地面多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 是线段
是线段![]() 的垂直平分线,交线段
的垂直平分线,交线段![]() 于点
于点![]() ,在
,在![]() 下方的直线
下方的直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ,以线段
,以线段![]() 为边,在
为边,在![]() 上方作正方形
上方作正方形![]() ,射线
,射线![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
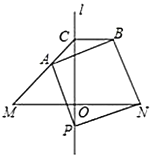
(1)设![]() ,求
,求![]() 的度数;
的度数;
(2)写出线段![]() 、
、![]() 之间的等量关系,并证明.
之间的等量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第![]() 天的成本
天的成本![]() (元/件)与
(元/件)与![]() (天)之间的关系如图所示,并连续50天均以80元/件的价格出售,第
(天)之间的关系如图所示,并连续50天均以80元/件的价格出售,第![]() 天该产品的销售量
天该产品的销售量![]() (件)与
(件)与![]() (天)满足关系式
(天)满足关系式![]() .
.
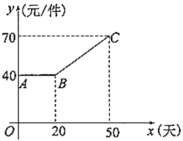
(1)第40天,该商家获得的利润是______元;
(2)设第![]() 天该商家出售该产品的利润为
天该商家出售该产品的利润为![]() 元.
元.
①求![]() 与
与![]() 之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
②在出售该产品的过程中,当天利润不低于1000元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某居民楼![]() 的前面有一围墙
的前面有一围墙![]() ,在点
,在点![]() 处测得楼顶
处测得楼顶![]() 的仰角为
的仰角为![]() ,在
,在![]() 处测得楼顶
处测得楼顶![]() 的仰角为
的仰角为![]() ,且
,且![]() 的高度为2米,
的高度为2米,![]() 之间的距离为20米(
之间的距离为20米(![]() ,
,![]() ,
,![]() 在同一条直线上).
在同一条直线上).
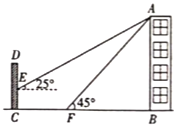
(1)求居民楼![]() 的高度.
的高度.
(2)请你求出![]() 、
、![]() 两点之间的距离.(参考数据:
两点之间的距离.(参考数据:![]() ,
,![]() ,
,![]() ,结果保留整数)
,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作三角形的高线”的尺规作图过程.

已知:△ABC.
求作:BC边上的高线.
作法:如图,
①分别以A,B为圆心,大于![]() 长为半径画弧,两弧交于点D,E;
长为半径画弧,两弧交于点D,E;
②作直线DE,与AB交于点F,以点F为圆心,FA长为半径画圆,交CB的延长线于点G;
③连接AG.
所以线段AG就是所求作的BC边上的高线.

根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:连接DA,DB,EA,EB,
∵DA=DB,
∴点D在线段AB的垂直平分线上( )(填推理的依据).
∵ = ,
∴点E在线段AB的垂直平分线上.
∴DE是线段AB的垂直平分线.
∴FA=FB.
∴AB是⊙F的直径.
∴∠AGB=90°( )(填推理的依据).
∴AG⊥BC
即AG就是BC边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
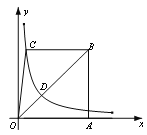
【题目】如图,已知梯形ABCO的底边AO在![]() 轴上,
轴上,![]() ,AB⊥AO,过点C的双曲线
,AB⊥AO,过点C的双曲线![]() 交OB于D,且
交OB于D,且![]() ,若△OBC的面积等于3,则k的值为__________.
,若△OBC的面积等于3,则k的值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com