
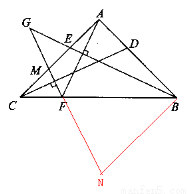
(12分)如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M。

(1)求证:△ADC≌△AEB ,
(2)判断△EGM是什么三角形,并证明你的结论;
(3)猜想线段BG、AF与FG的数量关系并证明你的结论。
(1)详见解析;(2)△EGM是等腰三角形,证明详见解析;(3)BG=AF+FG;证明详见解析
【解析】
试题分析:(1)∵等腰直角三角形ABC中,∠BAC=90°,
∴AC=AB,∠ACB=∠ABC=45°,
在△ADC和△AEB中
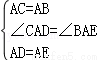
∴△ADC≌△AEB(SAS),
(2)△EGM为等腰三角形;
理由:∵△ADC≌△AEB,
∴∠1=∠3,
∵∠BAC=90°,
∴∠3+∠2=90°,∠1+∠4=90°,
∴∠4+∠3=90°
∵FG⊥CD,
∴∠CMF+∠4=90°,
∴∠3=∠CMF,
∴∠GEM=∠GME,
∴EG=MG,△EGM为等腰三角形.
(3)线段BG、AF与FG的数量关系为BG=AF+FG.
理由:如图所示:过点B作AB的垂线,交GF的延长线于点N,
∵BN⊥AB,∠ABC=45°,
∴∠FBN=45°=∠FBA.
∵FG⊥CD,
∴∠BFN=∠CFM=90°﹣∠DCB,
∵AF⊥BE,
∴∠BFA=90°﹣∠EBC,∠5+∠2=90°,
由(1)可得∠DCB=∠EBC,
∴∠BFN=∠BFA,
在△BFN和△BFA中
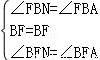
∴△BFN≌△BFA(ASA),
∴NF=AF,∠N=∠5,
又∵∠GBN+∠2=90°,
∴∠GBN=∠5=∠N,
∴BG=NG,
又∵NG=NF+FG,
∴BG=AF+FG.
考点:特殊三角形的综合运用


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:填空题
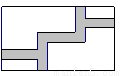
如图,在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪.要使草坪的面积为540米,则道路的宽为 米.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市八年级上学期期中考试数学试卷(解析版) 题型:选择题
下列实数3.14, ,π,
,π, ,0.121121112…,
,0.121121112…, 中,有理数有( )个.
中,有理数有( )个.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列说法中,正确的是( )
A.长度相等的两条弧是等弧
B.优弧一定大于劣弧
C.不同的圆中不可能有相等的弦
D.直径是弦且是同一个圆中最长的弦
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市邗江区八年级上学期期中测试数学试卷(解析版) 题型:解答题
(8分)如图,已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,求:∠AFD的度数?.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市邗江区八年级上学期期中测试数学试卷(解析版) 题型:填空题
如图,△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为 _____________。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市邗江区九年级上学期期中测试数学试卷(解析版) 题型:解答题
(本题满分12分)已知:如图等边△ABC内接于⊙O,点P是劣弧BC上的一点(端点除外),延长BP至D,使BD=AP,连接CD.

(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由.
(2)若AP不过圆心O,如图②,请你判断△PDC是什么三角形?并说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宝应县九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com