
在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
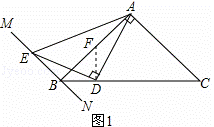
(1)如图①,当∠ABC=45°时,求证:AD=DE;
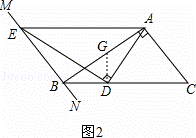
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)
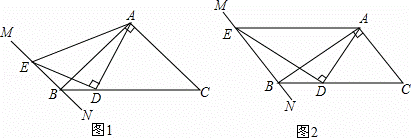
(1)证明:如图1,过点D作DF⊥BC,交AB于点F,
则∠BDE+∠FDE=90°,
∵DE⊥AD,
∴∠FDE+∠ADF=90°,
∴∠BDE=∠ADF,
∵∠BAC=90°,∠ABC=45°,
∴∠C=45°,
∵MN∥AC,
∴∠EBD=180°﹣∠C=135°,
∵∠BFD=45°,DF⊥BC,
∴∠BFD=45°,BD=DF,
∴∠AFD=135°,
∴∠EBD=∠AFD,
在△BDE和△FDA中
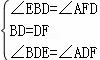 ,
,
∴△BDE≌△FDA(ASA),
∴AD=DE;
(2)解:DE= AD,
AD,
理由:如图2,过点D作DG⊥BC,交AB于点G,
则∠BDE+∠GDE=90°,
∵DE⊥AD,
∴∠GDE+∠ADG=90°,
∴∠BDE=∠ADG,
∵∠BAC=90°,∠ABC=30°,
∴∠C=60°,
∵MN∥AC,
∴∠EBD=180°﹣∠C=120°,
∵∠ABC=30°,DG⊥BC,
∴∠BGD=60°,
∴∠AGD=120°,
∴∠EBD=∠AGD,
∴△BDE∽△GDA,
∴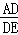 =
=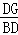 ,
,
在Rt△BDG中,
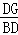 =tan30°=
=tan30°=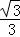 ,
,
∴DE= AD;
AD;
(3)AD=DE•tanα;
理由:如图2,∠BDE+∠GDE=90°,
∵DE⊥AD,
∴∠GDE+∠ADG=90°,
∴∠BDE=∠ADG,
∵∠EBD=90°+α,∠AGD=90°+α,
∴∠EBD=∠AGD,
∴△EBD∽△AGD,
∴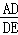 =
=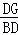 ,
,
在Rt△BDG中,
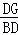 =tanα,则
=tanα,则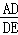 =tanα,
=tanα,
∴AD=DE•tanα.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A1B1C1.
(1)△ABC与△A1B1C1的位似比等于 ;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A1B1C1是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 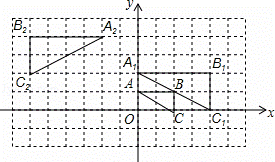
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com