
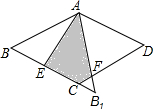
 如图,在边长为$\sqrt{2}$的菱形ABCD中,∠B=45°,AE是BC边上的高,将△AEB沿AE所在直线翻折得△AEB1,则△AEB1与四边形AECF重叠部分的面积为$\sqrt{2}$-1.
如图,在边长为$\sqrt{2}$的菱形ABCD中,∠B=45°,AE是BC边上的高,将△AEB沿AE所在直线翻折得△AEB1,则△AEB1与四边形AECF重叠部分的面积为$\sqrt{2}$-1. 分析 根据等腰直角三角形的性质求出BE、AE,根据翻转变换的性质得到△FCB1是等腰直角三角形,根据三角形的面积公式计算即可.
解答 解:∵AE⊥BC,∠B=45°,AB=$\sqrt{2}$
∴BE=AE=1,
∵将△AEB沿AE所在直线翻折得△AEB1,
∴∠B1=∠B=45°,
∴EB1=BE=1,CB1=2-$\sqrt{2}$,
∴△AEB1的面积为$\frac{1}{2}$×AE×EB1=$\frac{1}{2}$,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠FCB1=∠B=45°,
∴△FCB1是等腰直角三角形,
∴△FCB1的面积为$\frac{1}{2}$×(2-$\sqrt{2}$)×$\frac{1}{2}$×(2-$\sqrt{2}$)=$\frac{3}{2}$-$\sqrt{2}$,
∴△AEB1与四边形AECF重叠部分的面积=$\frac{1}{2}$-($\frac{3}{2}$-$\sqrt{2}$)=$\sqrt{2}$-1,
故答案为:$\sqrt{2}$-1.
点评 本题考查的是翻转变换的性质和菱形的性质,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


科目:初中数学 来源: 题型:填空题
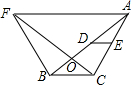 如图,△ABC是钝角三角形,DE是△ABC的中位线,现有△FCB≌△ABC,恰有AB⊥FC,垂足为O,连接AF,若DE=1.5,AF=7,则BC与AF之间的距离为5.
如图,△ABC是钝角三角形,DE是△ABC的中位线,现有△FCB≌△ABC,恰有AB⊥FC,垂足为O,连接AF,若DE=1.5,AF=7,则BC与AF之间的距离为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
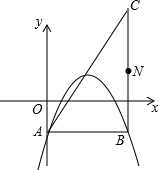 如图,在平面直角坐标系中,已知y=-$\frac{1}{2}$x2+bx+c(b、c为常数)的顶点为P,等 腰直角三角形ABC的顶点A的坐标为(0,-1),点C的坐标为(4,3),直角顶点B在第四象限.
如图,在平面直角坐标系中,已知y=-$\frac{1}{2}$x2+bx+c(b、c为常数)的顶点为P,等 腰直角三角形ABC的顶点A的坐标为(0,-1),点C的坐标为(4,3),直角顶点B在第四象限.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数$y=\frac{k}{x}$的图象上.求反比例函数解析式.
如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数$y=\frac{k}{x}$的图象上.求反比例函数解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在所给的平面直角坐标系中.
如图所示,在所给的平面直角坐标系中.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com