
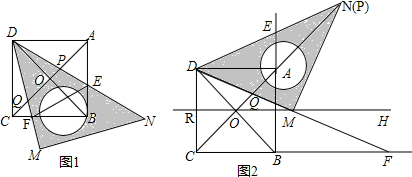
分析 (1)首先根据四边形ABCD是正方形,△DMN是等腰直角三角形,推得∠DAP=∠DBF,∠ADP=∠BDF,即可判断出△ADP∽△BDF;然后根据四边形ABCD是正方形,可得AD:BD=1:$\sqrt{2}$,据此判断出△ADP和△BDF相似比为1:$\sqrt{2}$即可.
(2)根据相似三角形的判定方法,即可推得两对相似比为1:$\sqrt{2}$的非直角三角形的相似三角形.
(3)①(2)中的结论仍然成立.根据相似三角形的判定方法,判断出∠DCQ=∠DBE,∠CDQ=∠BDE,即可判断出△CDQ∽△BDE;然后根据CD:BD=1:$\sqrt{2}$,即可推得△CDQ和△BDE的相似比为1:$\sqrt{2}$.
②首先作NG⊥RH于点G,根据全等三角形判定的方法,判断出△MGN≌△DRM,即可推得NG=MR,MG=DR,再根据DR=RO,推得MG=RO;然后根据MG+OM=RO+OM,推得RM=OG,在△ONG中,根据勾股定理,求出RM的长是多少即可.
解答 (1)证明:如图1,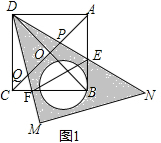 ,
,
∵四边形ABCD是正方形,
∴∠DAP=∠DBF=∠ADO=45°,
∴∠ADP+∠ODP=45°,
又∵△DMN是等腰直角三角形,
∴∠MDN=45°,
∴∠BDF+∠ODP=45°,
∴∠ADP=∠BDF,
在△ADP和△BDF中,
$\left\{\begin{array}{l}{∠DAP=∠DBF}\\{∠ADP=∠BDF}\end{array}\right.$
∴△ADP∽△BDF,
∵四边形ABCD是正方形,
∴AD:BD=1:$\sqrt{2}$,
∴△ADP和△BDF的相似比为1:$\sqrt{2}$.
(2)解:两对相似比为1:$\sqrt{2}$的非直角三角形的相似三角形△CDQ与△BDE,△DPQ与△DFE.
①如图2,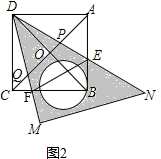 ,
,
∵四边形ABCD是正方形,
∴∠DCQ=∠DBE=∠CDO=45°,
∴∠CDQ+∠ODQ=45°,
又∵△DMN是等腰直角三角形,
∴∠MDN=45°,
∴∠BDE+∠ODQ=45°,
∴∠CDQ=∠BDE,
在△CDQ和△BDE中,
$\left\{\begin{array}{l}{∠DCQ=∠DBE}\\{∠CDQ=∠BDE}\end{array}\right.$
∴△CDQ∽△BDE,
∵四边形ABCD是正方形,
∴CD:BD=1:$\sqrt{2}$,
∴△CDQ和△BDE的相似比为1:$\sqrt{2}$.
②如图3,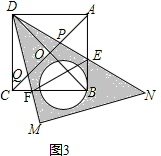 ,
,
∵△ADP∽△BDF,且相似比为1:$\sqrt{2}$,
∴DP:DF=1:$\sqrt{2}$,
∵△CDQ∽△BDE,且相似比为1:$\sqrt{2}$,
∴DQ:DE=1:$\sqrt{2}$,
∴DP:DF=DQ:DE,
又∵∠PDQ=∠FDE,
∴△DPQ∽△DFE,且相似比为1:$\sqrt{2}$.
(3)①解:(2)中的结论仍然成立.
如图4,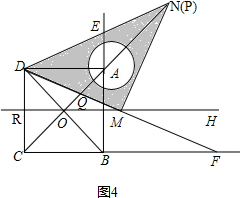 ,
,
∵四边形ABCD是正方形,
∴∠DCQ=∠DBE=∠CDO=45°,
又∵△DMN是等腰直角三角形,
∴∠MDN=45°,
∴∠CDO+∠ODQ=∠MDE+∠BDM,
即∠CDQ=∠BDE,
在△CDQ和△BDE中,
$\left\{\begin{array}{l}{∠DCQ=∠DBE}\\{∠CDQ=∠BDE}\end{array}\right.$
∴△CDQ∽△BDE,
∵四边形ABCD是正方形,
∴CD:BD=1:$\sqrt{2}$,
∴△CDQ和△BDE的相似比为1:$\sqrt{2}$.
②解:如图5,作NG⊥RH于点G,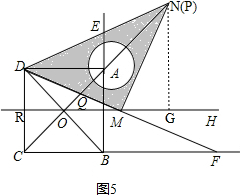 ,
,
∴∠MGN=90°,
∴∠GNM+∠NMG=90°,
∵∠DMN=90°,
∴∠RMD+∠NMG=90°,
∴∠GNM=∠RMD,
∵RH是AB的中垂线,
∴∠DRM=90°,
∴∠MGN=∠DRM,
∵△DMN是等腰直角三角形,
∴MN=DM,
在△MGN和△DRM中,
$\left\{\begin{array}{l}{∠GNM=∠RMD}\\{∠MGN=∠DRM}\\{MN=DM}\end{array}\right.$,∴△MGN≌△DRM,
∴NG=MR,MG=DR,
∵DR=RO,
∴MG=RO,
∴MG+OM=RO+OM,
∴RM=OG,
∵ON=6,∠NOG=45°,
∴RM=OG=6×$\frac{\sqrt{2}}{2}$=3$\sqrt{2}$.
故答案为:△CDQ、△BDE、△DPQ、△DFE.
点评 (1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.
(3)此题还考查了全等三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①判定定理1:SSS--三条边分别对应相等的两个三角形全等.②判定定理2:SAS--两边及其夹角分别对应相等的两个三角形全等.③判定定理3:ASA--两角及其夹边分别对应相等的两个三角形全等.④判定定理4:AAS--两角及其中一个角的对边对应相等的两个三角形全等.⑤判定定理5:HL--斜边与直角边对应相等的两个直角三角形全等.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:填空题
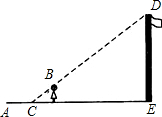 如图,小亮欲测量一建筑物的高度.他站在该建筑物的影子上,前后移动,直到他本身影子的顶端正好与建筑物影子的顶端重叠.此时,他距离该建筑物18米.小亮的身高是1.6米,他的影子长是2米,那么该建筑物的高度是16米.
如图,小亮欲测量一建筑物的高度.他站在该建筑物的影子上,前后移动,直到他本身影子的顶端正好与建筑物影子的顶端重叠.此时,他距离该建筑物18米.小亮的身高是1.6米,他的影子长是2米,那么该建筑物的高度是16米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 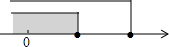 | ||
| C. | 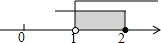 | D. | 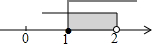 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x2-2) | B. | x(x-1)2 | C. | x(x-$\sqrt{2}$)(x$+\sqrt{2}$) | D. | x(x-$\sqrt{2}$)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com