
分析 由原方程得到:(a2+1)(b2+1)=5×401,由于a、b都是整数,所以由该等式得到方程组$\left\{\begin{array}{l}{{a}^{2}+1=5}\\{{b}^{2}+1=401}\end{array}\right.$或$\left\{\begin{array}{l}{{a}^{2}+1=401}\\{{b}^{2}+1=5}\end{array}\right.$,从而求出a、b的值.
解答 解:由a2b2+a2+b2=2004,得
a2+b2+a2b2+1=2004+1,
∴a2(b2+1)+(b2+1)=2005,
∴(b2+1)(a2+1)=5×401
∵a,b都是整数,
∴$\left\{\begin{array}{l}{{a}^{2}+1=5}\\{{b}^{2}+1=401}\end{array}\right.$或$\left\{\begin{array}{l}{{a}^{2}+1=401}\\{{b}^{2}+1=5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=±2}\\{b=±20}\end{array}\right.$或$\left\{\begin{array}{l}{a=±20}\\{b=±2}\end{array}\right.$.
综上所述,a的值为±2,b的值为±20;或a的值为±20,b的值为±2.
点评 本题考查了非一次不定方程(组),因式分解的应用.此题的难点是把已知等式转化为形式:(b2+1)(a2+1)=5×401.


科目:初中数学 来源: 题型:选择题
 我们学校教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:30)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
我们学校教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:30)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )| A. | 7:00 | B. | 7:07 | C. | 7:10 | D. | 7:15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
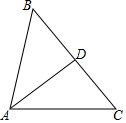 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )| A. | BD=DC,AB=AC | B. | ∠ADB=∠ADC,BD=DC | C. | ∠B=∠C,∠BAD=∠CAD | D. | ∠B=∠C,BD=DC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明给如图建立平面直角坐标系,使医院的坐标为(0,0),火车站的坐标为(2,2).
小明给如图建立平面直角坐标系,使医院的坐标为(0,0),火车站的坐标为(2,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,学校准备在教学楼后面搭建一简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为18m),另外三边利用学校现有总长38m的铁栏围成.
如图所示,学校准备在教学楼后面搭建一简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为18m),另外三边利用学校现有总长38m的铁栏围成.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com